60-265:%20Computer%20Architecture%201:%20Digital%20Design%20SIMPLIFICATION%20and%20IMPLEMENTATION

1
60-265 Computer Architecture 1 Digital
DesignSIMPLIFICATION and IMPLEMENTATION

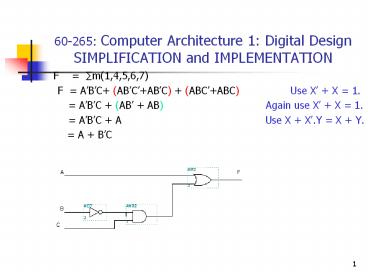
• F ?m(1,4,5,6,7)
• F ABC (ABCABC) (ABCABC)
  Use X X 1.
• ABC (AB AB)
  Again use X X 1.
• ABC A
  Use X X.Y X Y.
• A BC

2
Implementation of Inverter/AND/OR
using NAND gates only

• Inverter using NAND
• AND using NAND
• OR using NAND

3
IMPLEMENTATION of F A BC using
NAND gates only

• To implement the previous simplified function by
  using NAND gates only
• X NAND Y (X.Y)
• F (A B.C)
• ( (A B.C) )
• (A.(B.C))

4
Implementation of Inverter/AND/OR
using NOR gates only

• Inverter using NOR
• AND using NOR
• OR using NOR

5
IMPLEMENTATION of F A BC
using NOR gates only

• To implement the same function by using NOR gates
  only X NOR Y (X Y)
• F (A BC)
• ((A (BC)))
• ((A (BC) )) ((A P))

6
Variables, Literals and minterms

• Variables A, B or C of Variables n
• Literals A, A, B, B, C or C
• of literals 2n
• minterm ANDing of n literals such that if a
  literal x is present, its complement will not be
  present
• A minterm is equal to 1 for only one set of
  values of the variables. For all other sets of
  values of the variables, the minterm is equal to
  0.

7
Maxterms

• Maxterm ORing of n literals such that if a
  literal x is present, its complement will not be
  present
• A Maxterm is equal to 0 for only one set of
  values of the variables. For all other sets of
  values of the variables, the Maxterm is equal to
  1.

8
Examples minterm and Maxterms
for a Function of 3 variables

• A B C minterm F Maxterm
• 0 0 0 A.B.C 0 A B C
  
• 0 0 1 A.B.C 1 A B C
• 0 1 0 A.B.C 0 A B C
• 0 1 1 A.B.C 0 A B C
• 1 0 0 A.B.C 1 A B C
• 1 0 1 A.B.C 1 A B C
• 1 1 0 A.B.C 1 A B C
• 1 1 1 A.B.C 1 A B C

9
Defining a Function in terms of
minterms and Maxterms

• Definition F ? m(1,4,5,6,7) ? M(0, 2, 3)
• F represents an output function, which
  is equal to 1 for the rows with equivalent
  decimal value of 1, 4, 5, 6 and 7 and which is
  equal to 0 for the rows with equivalent decimal
  value of 0, 2 and 3.
• F A.B.C A.B.C A.B.C A.B.C A.B.C
• (A B C).(A B C).(A B C)

10
Ex. 2 SIMPLIFICATION and IMPLEMENTATION

• F X.Y.Z X.Y.Z X.Y.Z
• (XX).Y.Z X.Y.Z
  Use X X 1.
• Y.Z X.Y.Z (Y Y.X).Z (YX).Z Use X
  X.Y X Y.
• To implement using NAND gates only F
  (Y.ZX.Z)
• F ( (Y.Z) . (X.Z) ) (A.B)

11
Combinatorial Circuits

• Combinatorial Circuit A circuit, the outputs of
  which depend upon only the present values of the
  inputs only ( and not on the history of the past
  values of the inputs or outputs.)
• Characteristic Table shows the binary
  relationship between the n input variables and m
  output variables.
• For n variables, the Characteristic Table has
  2n entries.

1
1
m
n
Half-adder
A
S
HA
C
B
Full-adder
X
S
FA
Y
C
Z
12
Combinatorial circuit Half-Adder

• Half Adder It performs the arithmetic addition
  of two bits.
• Symbols A and B for two input variables , S for
  sum and C for carry.
• A B S C
• 0 0 0 0
• 0 1 1 0
• 1 0 1 0
• 1 1 0 1
• C A .B
• S AB AB A ? B

13
Combinatorial circuit Full-Adder

• Full Adder

x
Cout

y
S
Cin
X Y Cin S Cout 0 0 0 0 0 0
0 1 1 0 0 1 0 1 0 0 1
1 0 1 1 0 0 1 0 1 0
1 0 1 1 1 0 0 1 1 1 1
1 1 Truth Table for Full-Adder
It performs the arithmetic addition of three
input bits.
Cout x.y.Cin x.y.Cin x.y.Cin x.y.Cin
(x.y x.y).Cin (CinCin)x.y
( x.y x.y ). Cin x.y (x ?
y).Cin x.y
14
Combinatorial circuit Full-Adder

• S x.y.Cin x.y. Cin x.y. Cin
  x.y. Cin
• (x.y x.y). Cin (x.y x.y).
  Cin
• (x.yx.y). Cin (x ? y). Cin
• Q.Cin P.Cin
• If Q were equal to P
• S P.Cin P.Cin
• P ? Cin
• (x ? y) ? Cin
• To see if it is so
• P x.y x.y
• P (x y).(x y)
  Use De Morgans Theorem
• x.x x.y x.y y.y
• x.y x.y
• Q

15
Combinatorial circuit Full-Adder circuit

• Full-adder circuit

16
Combinatorial circuit continued

• .

F1
0
Boolean inputs
outputs
F2
N-1
The input set has 2n distinct terms. For each
output, find F1 fn1(I0 ....In-1.)
F2 fn2(I0
....In-1.) For implementing the logic functions,
the basic issue is of simplification. No
specific rules for determining the sequence of
steps or the specific theorems that may be
used. Karnaugh Map ----- graphical method The
number of cells 2n --- Each cell
corresponds to a minterm. Adjacent cells differ
by only one bit.