7.7 MASS LUMINOSITY RELATIONSHIP

1
7.7 MASS LUMINOSITY RELATIONSHIP
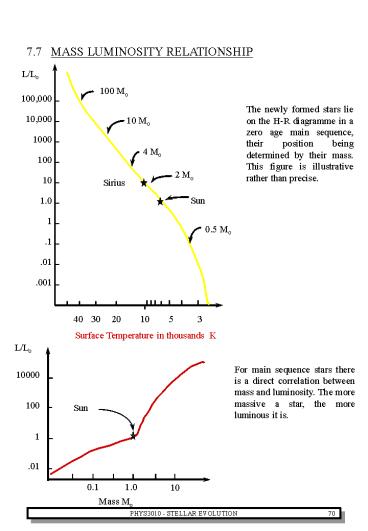
The newly formed stars lie on the H-R diagramme
in a zero age main sequence, their position being
determined by their mass. This figure is
illustrative rather than precise.
L/Lo
For main sequence stars there is a direct
correlation between mass and luminosity. The more
massive a star, the more luminous it is.
10000
100
Sun
1
.01
0.1
1.0
10
Mass Mo
2
MAIN SEQUENCE STARS Some Generalised Parameters
The above table illustrates the wide range (
106) of luminosities that are produced in main
sequence stars for what is effectively a very
narrow range of masses ( 100). Note also the
wide range ( 105) of the stars lifetime on the
main sequence.
3
7.8 THE SUN LIKELY INTERNAL STRUCTURE
Thermonuclear energy core
Radiative Zone
X-rays
Convective Zone
g-rays
Thermonuclear reactions occur in the Suns core,
which extends out to about 0.25 Ro from the
centre. Energy is transported outwards via
radiative transport to a distance of 0.8 Ro.
Convection is responsible for energy transport in
the Suns outer layers. Note the neutrinos escape
with their energy.
4
15 106
10 106
Temperature (K)
5 106
0.2
0.4
0.6
0.8
1.0
150
1
Density (g/cm2)
0.01
.0001
0.2
0.4
0.6
0.8
1.0
Distance from the Suns centre (solar radii)
The above figures illustrate the internal
structure of the Sun as given in the previous
table, they show how the density, temperature,
mass, and luminosity are likely to vary with
distance from the Suns centre.
5
7.9 THE CHEMICAL COMPOSITION OF THE SUN
Whereas the Sun began with a composition of
nearly 75 hydrogen and 25 helium, after 5
billion years of thermonuclear reactions at the
Suns centre have depleted the concentration of
hydrogen and increased that of helium.
6
8. EVOLUTION OFF THE MAIN SEQUENCE
The main sequence represents a long period of
high stability for stars during which hydrogen is
converted to helium. Note that the main sequence
is not an evolutionary track. The position of a
star on the main sequence is almost entirely
determined by the mass of the star. As we have
seen from the linear model the luminosity of a
star is a high power of the mass, hence the main
sequence simply reflects the mass distribution of
hydrogen burning stars.
L
mass
T
The main sequence is not a line on the H-R
diagramme, but rather a band as illustrated in
the figure. This reflects the fact that all stars
are not identical. The composition m is the main
factor which causes differences in luminosity for
the same stellar mass. Having (hopefully) made it
clear that the main sequence is not an
evolutionary track, one should note that, since
during the main sequence phase hydrogen does get
converted to helium, the composition will change.
This will have an impact on the reaction rates
etc. and thus modify the luminosity. Thus during
its main sequence lifetime minor changes of the
stars position on the H-R diagramme are expected.
NOTE
i) Observationally, the study of evolution off
the main sequence has the problem that the age of
the Galaxy is finite and corresponds to the
lifetime of a 1.5 M0 star. Thus it is
impossible to observe, from within our own
galaxy, what happens to stars at the lower end of
the mass range. ii) The time required for a star
to evolve through the stages subsequent to the
main sequence is short compared to its total
lifetime. Consequently there are less examples
available for study. iii) The post main sequence
evolution is more complex, there is more
interplay between the various parts of the star,
detailed analytical modelling is not practical.
7
8.1 SHELL BURNING SOURCES AND THE CENTRAL
CONDENSATION
The figure gives a schematic representation of
the evolutionary tracks of a one solar mass and
a ten solar mass star after the main
sequence. The table below gives an approximate
indication of the period of time the star spends
during each phase of evolution after the main
sequence. The periods are measured in years.
6
L
5
4
3
4
2
1
10 Mo
3
2
1
1 Mo
T

• Initially, as the composition changes the stars
  will move slightly within the main sequence band.
  The change in the value of m and its strong
  influence on the luminosity causes the luminosity
  and temperature to increase. (1) This period
  represents a large fraction of their lifetime
  within the main sequence band.

• As the hydrogen content is burnt away helium
  builds up to form a helium rich core to the star.
  The H burning will then be confined to a shell
  around a growing core of pure He. The star is
  now effectively leaving the main sequence. Since
  the temperature is not sufficiently high at this
  stage no thermonuclear helium burning takes place
  in the core. The core will be isothermal. It
  contracts since this is the only way it can
  maintain the thermal pressure required to support
  the ever increasing amount of He. This
  contraction raises the temperature. (2)

H burning shell
Remaining envelope
He
8

• The adiabatic increase in temperature of the
  core due to contraction increases the rate of
  hydrogen shellburning which in turn increases the
  the rate of energy release. (remember the G µ Tn
  dependence of thermonuclear reactions) The
  increased luminosity causes the outer layers of
  the star to expand through radiation pressure.
  The increased luminosity means that the track
  should move upwards on the figure, but the
  expansion of the size of the envelope is more
  pronounced, energy is absorbed and the luminosity
  actually drops. The expansion also increases the
  radiating surface area of the star which further
  causes the surface temperature to drop. The star
  moves to the right on the figure. (3) The
  timescale of this period is somewhat shorter than
  the earlier and later phases so that less stars
  are seen in this region of the H-R diagramme.
  (Hertzsprung Gap) Note from the table that the
  Hertzsprung gap will be more pronounced for
  higher mass stars due to the correspondingly
  shorter interval of time. The Hertzsprung gap
  separates the main sequence from the red giants
  and is clearly evident in the H-R diagrammes for
  clusters. It is a transitory phase before the
  true Red Giant phase.

The outline internal structure of a low (1)
solar mass star at the point (3) is shown
schematically in the figure. The He core
comprises about 10 of the mass of the star M.
The H-burning shell, indicated from dL/dm, is
quite thin and close to the centre (r/R 0.3).
The drop in temperature and luminosity in the
outer envelope is clearly seen.
9

• The increased ash from the shell burning causes
  the core to be more and more compressed. It will
  suffer more contraction which further increases
  the temperature. There will be a corresponding
  increase in the shell burning and even more
  radiation produced. The expanded envelope
  becomes cooler and has increased opacity, it will
  no longer be in radiative equilibrium and becomes
  highly convective, expanding even further. The
  core becomes degenerate towards the centre and is
  partially supported by degeneracy pressure. (See
  later discussion relating to white dwarfs) The
  star is now a Red Giant. (4) The core parameters
  for a low mass star at this stage are indicated
  below

m(r)/M
NOTE
The detailed physics and hence the evolutionary
tracks are very much dependent upon the mass of
the star. Here only an approximate outline of the
evolutionary process is indicated. Space
precludes a detailed discussion of the various
options. Students are strongly advised to read
more detailed accounts in the referenced
literature provided.
10
8.2 INTERNAL STRUCTURE OF A RED GIANT
Hydrogen burning shell
Isothermal Helium core
Hydrogen burning core
The Sun as a main sequence star Diameter 1.4
109 m
Convective envelope
The Sun as a Red Giant, diameter 1.4 1010 m
The structure is as shown. The electron
degeneracy at the centre makes the core an
excellent conductor which ensures the isothermal
nature of the core. Red giants are relatively
cool on the outside. At the centre
r 108 kg m-3, T 108 K
Note that the outer radius of a red giant will
extend roughly out to the radius of the Earths
orbit around the Sun.
11
TRIPLE a PROCESS
With a central core temperature of typically 2
108 K the triple a process becomes important. Two
a particles can form the short-lived Be8 isotope
When the density is high enough another
a-particle can be absorbed during this period.
This enhanced reaction cross-section is of major
importance, since without it the entire process
of stellar evolution would be entirely different,
and the Universe as we know it would not exist.
Also
And is capable of producing equal quantities of
C12 and O16. This process clearly accounts for
the high universal abundances of these elements.
The mass of the star determines what will happen.
For low mass stars (M sets in before ignition. When the helium does
ignite under degenerate conditions, the energy
release increases the temperature but not the
pressure (see under later discussion of white
dwarfs) and thermal runaway occurs. This is
called the Helium Flash. The heating does
eventually destroy the degeneracy and the core
will expand. In the case of high mass stars the
helium will undergo thermonuclear fusion before
electron degeneracy sets in.
12
8.3 MORE MASSIVE STARS
H shell burning source
More massive stars have higher central
temperatures and can be capable of burning higher
z-value isotopes. For example if the helium
burning takes place, then there will be two
burning regions the central helium burning region
and an hydrogen burning shell. A carbon core
could build up, and if the star were massive
enough to create a high enough temperature then
we can envisage a carbon core with both a helium
burning shell and a hydrogen burning shell.
He
Hydrogen
He shell source
Carbon
A star that is burning helium can be thought of
as a helium main sequence star. (point 5) However
the hydrogen burning shell source provides six
times as much energy as the helium core so that
the analogy is very approximate.
The internal structure of a star at this point is
outlined in the adjacent figure. The helium core
burning creates about 15 of the luminosity more
or less at the centre of the star.
A subsequent contraction (6) of the central core
as the helium burning ends has the same sort of
effect as the situation at the end of the
hydrogen burning main sequence phase. (3). The
evolutionary path can zig-zag in a similar manner
as the 3 - 4 - 5 effect.
13
8.4 DEVIATIONS FROM STABILITY - VARIABLE STARS -
MASS LOSS
All stars exhibit some kind of variability during
their lifetime. This may be due to such things as
the 11 year solar cycle, binary motions and
interactions, or something more catastrophic such
as a supernova explosion and so on. However some
stars are intrinsically more variable than others
due to their physical condition. In this section
we look at stars that are not only variable but
which undergo periodic changes in brightness.
There are a number of these, RR-Lyrae stars, long
period variables, and the Cepheids. These notes
will concentrate on the latter, mainly because of
their great importance in the measurement of
astronomical distances.
Long period variables
Classical Cepheids
The the positions of the major types of
intrinsically variable stars are shown on the H-R
diagramme. We see that they are situated above
the main sequence line, and are therefore very
extended post main sequence objects. We have
seen that after evolution off the main sequence
stars become very extended due to increased
radiation pressure. Note also that the
gravitational force on the outer layers will also
be considerably weaker.
L
Pop II Cepheids
RR-Lyrae
Tc
T
Two major effects arise 1) Mass loss from the
star is more easily accomplished 2) The
free-fall timescale
becomes longer due to the decreased density and
can become comparable to the thermal timescale.
This is the underlying reason why Cepheids are
variable.
14
8.5 CEPHEID VARIABLES AND THE MEASUREMENT OF
DISTANCE

• Cepheid variables are the most significant in
  this group because of their great importance in
  the field of astronomical distance measurement.
  The period of the variability cycle is
  proportional to their luminosity. This means that
  having calibrated the period luminosity
  relationship, one only needs to measure the
  period and the apparent brightness of the star to
  estimate its distance. However life is never
  quite that simple and the emission
  characteristics of Cepheids are not all precisely
  the same. In the context of distance measurement
  
• Because they are very luminous, they are visible
  out to large distances.
• The ESA astrometry mission Hipparcos has
  recently generated more precise distance
  measurements through parallax and hence will
  improve the luminosity-distance calibration.
• The Hubble Space Telescope has recently been
  able to identify and measure the brightness and
  period of Cepheids in distant galaxies, thus
  improving the estimate of the Hubble constant.

The Pulsation Mechanism
The Doppler measurements of line emissions from
Cepheids show that the pulsations are derived
from radial motions of the star. The mechanisms
exiting the pulsations are related to the
conversion of luminous energy into kinetic
energy. The heat energy is trapped during the
compressional phase and released during the
expansion stage. This keeps the clock ticking.
In the giant phase the temperature of the stars
are such that the opacity increases with
increasing temperature and the radiation cant
get out. Cepheids have their temperatures (Tc)
just at this point. When the star contracts
adiabatically its temperature rises, the opacity
increases and the radiation is trapped. This
energy eventually builds up and drives the star
outwards by radiation pressure. The star will
overshoot its natural equilibrium position at
about the point at which the gas becomes
transparent due to the decreased opacity. The
radiation is released, the star falls back and
compresses the gas once more.
15
Light Curves of Cepheid Variables
The above curves of the light emission, colour,
radial velocity and size illustrate the dynamics
of Cepheid pulsations. The required opacity
characteristics dictate that the stars lie on a
narrow band in the H-R diagramme. Note there are
two main types of Cepheids. The classical
Cepheids are derived from stars similar to the
Sun, i.e. Population I stars, whereas the
Population II Cepheids are, as may be expected,
associated with Globular clusters and older
stars. The different composition effects the
opacity relationships and eventually the
pulsational characteristics.
16
8.6 THE PERIOD LUMINOSITY RELATIONSHIP
The period of a Cepheid variable star is directly
related to its average luminosity. Metal rich
(Type I) Cepheids are brighter than the metal
poor (Type II) Cepheids. Type II Cepheids are
also called W Virginis stars.
If we assume that the pulsations are adiabatic
i.e. the pulsation periods are short compared to
the timescale required to reach thermal
equilibrium, then using
we have
we may crudely approximate the equation of
hydrostatic equilibrium as
17
Let us look at the effect a small change dR has
on the equilibrium of the star.
From 1 above
Substituting dr from 2 gives
The buoyancy force per unit mass is
from 2
The buoyancy force acts upwards
The gravitational force per unit mass is
So that for a slight perturbation of the star
18
The net force will produce an acceleration
and substituting
we obtain
which represents Simple harmonic Motion with
or period
NOTE

• The free-fall timescale is
• The magic 4/3 value of g will stop oscillations.
  A displacement under these conditions will grow
  with

19
The Period Luminosity Relationship
Having derived the period density relationship
for radially pulsating stars it is a
straightforward matter to obtain a
period-luminosity relationship
Since the period
and the density is
The radius may be eliminated by using the
definition of the effective temperature
and we obtain
giving
so that if T and M are expressed in terms of
luminosity we obtain the period luminosity
relationship. If we express this relationship in
terms of absolute visual magnitude rather than
luminosity, the following expression provides a
reasonably accurate description of the Cepheid
variations
20
HST CEPHEID VARIABLE IN M100
The galaxy M100 resides in the Virgo cluster, and
the HST measurements on the Cepheid variable
illustrated above has established the distance to
this cluster to be 56 million light years /- 6
million light years. In turn this means that the
Universe is expanding at a rate of 80 /- 17 km
s-1 Mpc-1. This constant is commonly known as the
Hubble Constant.