Applications to Deformations in Structures - PowerPoint PPT Presentation
1 / 18
Title:
Applications to Deformations in Structures
Description:
External Work done by forces on structure = internal Strain Energy ... Solve the truss using statics to determine the forces in each member: ... – PowerPoint PPT presentation
Number of Views:52
Avg rating:3.0/5.0
Title: Applications to Deformations in Structures
1
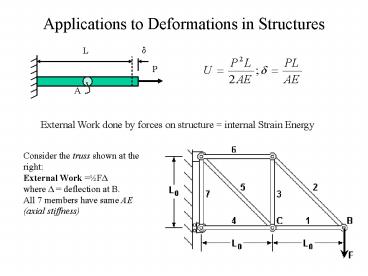
Applications to Deformations in Structures
d
L
P
A
External Work done by forces on structure
internal Strain Energy
Consider the truss shown at the right External
Work ½FD where D deflection at B. All 7
members have same AE (axial stiffness)
2
This assumes that the system is linear-elastic,
and therefore the deflection D is a linear
function of F.
Load, F
D, Deflection at B
The total strain energy stored in the system is
the sum of the individual strain energies in each
of the truss members numbered i1 to 7.
3
Equating External Work to Internal Strain Energy
DB
Since, in this case, EA is constant for all
members,
4
Try it!
A lightweight aluminum truss, E70000 MPa, has a
height, Lo1m, and is made of tubular stock with
a cross sectional area of 250 mm2. Determine the
deflection at B when the load, F20kN.
OK!.. Lets use an Energy method!
5
Solution
Solve the truss using statics to determine the
forces in each member
Note It doesnt matter if the axial load is
compressive or tensile, both add to the total
strain energy since the P term is squared.
6
OK, already find the deflection.
What is the maximum stress in the truss? P4
-2F40kN (compression) SP/A 40000/250 160
MPa ? assumptions about linear elasticity are OK,
if Sygt160MPa
7
Beam Elements
F(x)
x
z
y
dA
dx
y
y
A beam that is symmetrical in x-section about the
z-axis, is subjected to bending. Consider a
infinitesimal volume element of length dx and
area dA as shown. This element is subjected to a
normal stress sxMy/I The Strain Energy Density
on this element is
For linear elastic material
8
Substituting,
and multiplying by the Volume of the element
Hence, the Strain Energy for a slice of the beam,
of width dx, is
x
dx
y
9
Assumptions.
- There is no axial force on the element (case of
pure bending) - The shear stress strain on the element is
relatively small, and hence the contribution of
shear strain energy is negligible. - These assumptions are generally valid for long
slender beams.
10
Strain Energy in Entire Beam
Consider the cantilever beam as shown
F
L
x
d
I
y
11
Deflection
F
L
x
Linear-elastic, F ? d
d
I
y
Strain Energy
External Work,
Classical Solution
12
Try it!
P
x
Determine Elastic Strain Energy due to bending
for simply supported 3-point bending member of
constant X-section.
L/2
L/2
y
P/2
Shear Force
-P/2
For 0 ? x?L/2 MPx/2
PL/4
Note by symmetry we can find the total strain
energy by doubling the strain energy of the LHS.
Moment
13
P
DB
L/2
L/2
y
Determine DB.
14
DB can be determined by an energy method.
Izzbh3/12
z
h50mm
y
b20 mm
Find the Deflection for the x-section shown
L2m, P20 kN h50mm, b20mm, SAE1045 Steel,
E200,000 MPa, Sy400MPa
lt Sy , OK
15
Elastic Strain Energy due to Transverse Shear
Stress
y
txy
x
gxy
d gxya
16
Shear Strain Energy
F(x)
x
z
y
dA
dx
y
f is called a form factor Circle
f1.11 Rectangle f1.2 Tube f2.00 I
section fA/Aweb
17
Try it.
P
x
Determine Elastic Strain Energy due to shear
strain for simply supported 3-point bending
member of constant X-section.
L/2
L/2
y
P/2
Shear Force
-P/2
For 0 ? x?L/2 TP/2
PL/4
Note by symmetry we can find the total strain
energy by doubling the strain energy of the LHS.
Moment
18
z
h2c
for rectangle x-section
y
bmm
Izzbh3/12 Abh
For most metals G?0.4E we find that
And for slender beam, L/h10
which may be neglected