quantum parallelism

1
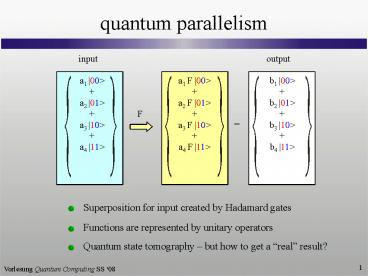
quantum parallelism
Superposition for input created by Hadamard gates
2
Deutsch algorithm table of truth
D. Deutsch, Proceedings of the Royal Society of
London A 400 (1985), 97
simplest example 1-bit-to-1-bit function f x ?
0,1
false
true
real or false?
3
strength of quantum parallelism
calculate a function f(x) with x ? 0,,K for
all x at once
classical
quantum
function balanced(Uffunction) Y?1 H Y?0 H
0?1? Y?2 Uf Y?1 Y?3 Hx Y?2
f(0)?f(1)?R? return f(0)?f(1)?
function balanced(ffunction) af(0) bf(1) return
a ? b
use quantum computing only if f(x) is expensive
to calculate (time, memory), e. g., spin dynamics
for huge structures
problem superposition cannot be read-out it
will always collapse to an eigenstate
4
Deutsch algorithm principle
input eigen- state 0?
read- out eigen- state
super- position 0? 1?
transfer to eigen- state 0? or 1?
one run only!
5
quantum circuit
data register
y?
y?
0?
target register
addition modulo 2 f(x) for y0
evaluation of function f(x) with n data qubits x
and 1 target qubit
BUT How to extract information?
6
Deutsch algorithm quantum circuit
Y0? 01?
Y2? Uf Y1?
7
Deutsch algorithm find Uf
Uf x,y? x,y?f(x)?
f(0)
f(1)
Uf
CNOT
Z-CNOT
NOT
ID
8
Deutsch algorithm get the answer
Y3? Hx Y2?
read-out
9
Deutsch algorithm summary
evaluates a global property of a function f(x)
with a single run
Y0? 01?
10
Deutsch algorithm implementation
Roos et al Phys. Rev. Lett. 83, 4713 (1999)
40Ca
11
Deutsch algorithm implementation
Gulde et al Nature 421, 48 (2003)
case 1 Uf ID
case 2 Uf NOT
case 3 Uf CNOT
case 4 Uf Z-CNOT
12
composite pulses
M. H. Levitt Prog. Nucl. Magn. Reson. Spectrosc.
18 (1986)
example imprecise B1-field
rotate from z to -z
1) p pulse at y (180y)
2) three pulse sequence 90y180x90y
13
Deutsch algorithm Fidelity
Gulde et al Nature 421, 48 (2003)
14
more than 1 ion
Nägerl et al Phys. Rev. A 60, 145(1999)
switching between ions within 14 ms
15
CNOT with 2 ions
Schmidt-Kaler et al Nature 422, 408(2003)
3mm
Control
Target
Y0? 01?
Y0? 01?
R(p,0)
gtY1? 10?
gtY1? 00?
R(p,p)
gtYe? 01?
CNOT spin state changed for n0
gtYe? 01?
16
CNOT with 2 ions
Schmidt-Kaler et al Nature 422, 408(2003)
3mm
Control
Target
Y0? 01?
Y0? 01?
gtY1? 01?
R(p,0)
gtY1? 11?
R(p,0)
gtY2? 11?
CNOT spin state changed for n0
R(p,p)
gtYe? 11?
gtYe? 11?
17
error sources
Schmitd-Kaler et al Nature 422, 408 (2003)
CNOT with 2 40Ca ions as qubits and vibration
mode as coupling
source
contribution
18
Needle in a haystack
Grover algorithm search in an unsorted database
Lov Grover, Bell labs
Quantum mechanics helps in searching for a
needle in a haystack
Phys. Rev. Lett. 79, 325 (1997)
19
Search in a database
Example search for a specific number in a
phonebook
We need

• N 2n entries with index x 0N-1.

• A detector function f(x)

20
The oracle
Grovers algorithm minimizes calls to oracle
Classical on average N/2 calls to oracle.
Quantum number of calls ? vN.
0
1
0
0
f(x)1 if entrance is solution
x? adresses of data register
00?
01?
10?
11?
21
Quantum circuit
Data register superposition of n2 qubits x?
Y1? 0?
f(x) 1
Target register oracle qubit q? prepared in
Y1? 1?
22
Oracle operator
x?
f(x) 0
UO
x?
x?
?x?
f(x) 1
UO x? q0? (-1)f(x) x? q0?
23
Grovers algorithm
Oracle qubit does not change Look at data
register only.
Y2?
Y3.4? H?2Y3.3?
01?
24
Grovers algorithm
H
H
H
H
UO x? q0? (-1)f(x) x? q0?
25
Geometrical analysis
a?
Superpostion of no-solutions
Superpostion of solutions
Y2? a? b?
Y2?
cos a? sin b?
26
Geometrical analysis
cos a? - sin b?
UO Y2?
Y2?
relexion at Y2?
27
Iterations
Necessary number R of iterations is CI to
p - Q
p
-
2 Q
2 Q
p
p
-
-
R ?? CI

2 Q
4 arcsin

• For more iterations than R, error increases

gt One needs to know number M of solutions.
28
ion trap quantum computing a summary

• qubit representation
• hyperfine states (9Be, 43Ca)
• electronic states (40Ca)
• vibrational modes
• qubit manipulation laser irradiation
• initial state preparation
• Doppler and sideband cooling
• read-out fluoresence

29
relaxation and operation

• electronic states
• energy relaxation time T1 1s
• phase relaxation time T2 10 ms
• gate operation time Tgate 200 ms
• T2/Tgate 50
• hyperfine states
• phase relaxation time T2 10s
• gate operation time Tgate 10 ms
• T2/Tgate 106

source Homepage group A. Steane
http//www.physics.ox.ac.uk/users/iontrap/news.htm
l
30
scaling to more than 10 ions
Kielpinski, Monroe, Wineland Nature 417, 709
(2002)