Geometric Design of Highways

1
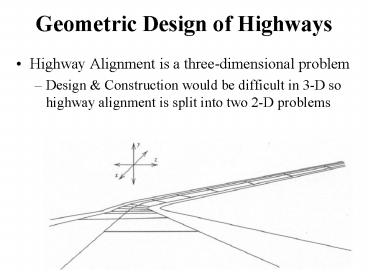
Geometric Design of Highways

• Highway Alignment is a three-dimensional problem
• Design Construction would be difficult in 3-D
  so highway alignment is split into two 2-D
  problems

2
Components of Highway Design
Horizontal Alignment

• Plan View

Vertical Alignment
Profile View
3
Horizontal Alignment

• Todays Class
• Components of the horizontal alignment
• Properties of a simple circular curve

4
Horizontal Alignment
Tangents
Curves
5
Tangents Curves
Tangent
Curve
Tangent to Circular Curve
Tangent to Spiral Curve to Circular Curve
6
Layout of a Simple Horizontal Curve

• R Radius of Circular Curve
• BC Beginning of Curve
• (or PC Point of Curvature)
• EC End of Curve
• (or PT Point of Tangency)
• PI Point of Intersection
• T Tangent Length
• (T PI BC EC - PI)
• L Length of Curvature
• (L EC BC)
• M Middle Ordinate
• E External Distance
• C Chord Length
• ? Deflection Angle

7
Circular Curve Components
8
Properties of Circular Curves

• Degree of Curvature
• Traditionally, the steepness of the curvature
  is defined by either the radius (R) or the degree
  of curvature (D)
• Degree of curvature angle subtended by an arc
  of length 100 feet
• R 5730 / D
• (Degree of curvature is
• not used with metric units
• because D is defined
• in terms of feet.)

9
Properties of Circular Curves

• Length of Curve
• For a given external angle (?), the length of
  curve (L) is directly related to the radius (R)
• L (R?p) / 180
• R? / 57.3
• In other words, the longer the curve, the larger
  the radius of curvature

R Radius of Circular Curve L Length of
Curvature ? Deflection Angle
10
Properties of Circular Curves

• Other Formulas
• Tangent T R tan(?/2)
• Chord C 2R sin(?/2)
• Mid Ordinate M R R cos(?/2)
• External Distance E R sec(?/2) - R

11
Circular Curve Geometry