NPcomplete Problems

1
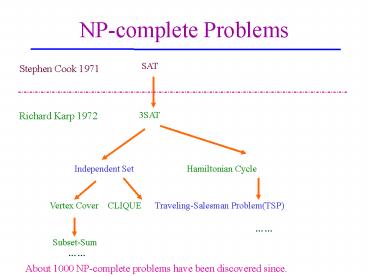
NP-complete Problems
SAT
Stephen Cook 1971
Richard Karp 1972


About 1000 NP-complete problems have been
discovered since.
2
Independent Set
Let G be an undirected graph.
A ? V(G) is an independent set if no two vertices
in A share an edge.
? u, v ? A, (u, v) ? E(G)
e
Ex.
d
a
g
A a, d, e, g is an independent set.
B a, c, f is not
3
The Independent-Set Problem
IND-SET
Input Graph G, integer K ? 1.
Q Does G have an independent set of size ? K ?
Theorem IND-SET is NP-complete.
Proof ? IND-SET ? NP. Below is a
non-deterministic algorithm
a) Pick K vertices from V(G) to form a subset A ?
V.
non-deterministic O(K) time
certificate
b) Check if ? u, v ? A, (u, v) ? E(G). If
so answer Yes otherwise, answer No.
4
3SAT IND SET
P
Proof (contd)
? We show that 3SAT is polynomial-time reducible
to IND-SET.
This will follow from Lemma 1.
Therefore IND-SET is NP-complete.
5
Constructing G
?
? One vertex for each literal.
? Literals in the same clause form a triangle.
? Opposite literals share edges.
6
Satisfiability vs. Independent Set
Lemma 1 ? satisfiable ? G has an independent
set of size K ( clauses in
?).
Proof ( ? ) Suppose ? is satisfiable.
Then at least one literal from every clause is
true. Pick exactly one such literal from each
clause and pick its corresponding vertex.
? K vertices are picked
? For two of these vertices to share an edge,
the corresponding literals would be
? either in the same clause
Impossible given the way these vertices are picked
? or opposite literals.
Impossible given that ? is satisfiable.
So none of the K vertices are adjacent.
Thus the K vertices form an independent set.
7
Contd
? do not include a pair of opposite literals.
Now we assign T to the corresponding literals in
?,
which will be true under the induced truth value
assignment to the variables.
8
Vertex Cover
Let G be an undirected graph.
a
C ? V 1
complete graph with n vertices
d
a, d is a vertex cover.
9
The Vertex Cover Problem
Vertex Cover (VC)
Input Graph G (V, E), positive integer K ?
V .
Q Does G have a vertex cover of size ? K ?
Lemma C is a vertex cover ? V C is an
independent set.
Proof (?) Let C be a vertex cover.
Suppose V C is not an independent set.
Then there exists two vertices u, v ? V C such
that (u, v) ? E.
a, d vertex cover
So edge (u, v) has both vertices not in C and C
is not a vertex cover.
(? ) Similarly.
b, c, e independent set
10
VC is NP-complete
Corollary IND-SET ? VC
P
It is easy to show that VC ? NP.
Theorem VC ? NPC.
11
CLIQUE
A clique Q is a subset of vertices such that
(u, v) is an edge for every u, v ? Q.
cliques a, b, c, d
e, f, g
d, e
g ,
The subgraph induced by Q is a complete graph.
12
Complement of a Graph
The complement G? of a graph G (V, E) has
? the same vertex set V
? edge set E? such that
(u, v) ? E? ? (u, v) ? E
Complement
Original graph
13
The CLIQUE Problem
Input Graph G (V, E), positive integer K ?
V .
Q Does G have a clique of size ? K ?
Lemma Q is a clique in G ? Q is
an independent set in the complement G? .
Theorem CLIQUE ? NPC.