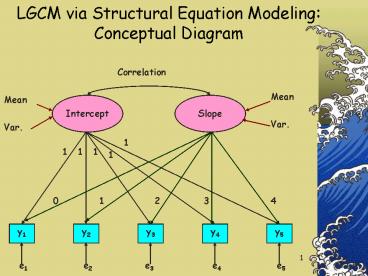
LGCM via Structural Equation Modeling: Conceptual Diagram

1
LGCM via Structural Equation Modeling Conceptual
Diagram
Correlation
Mean
Mean
Intercept
Slope
Var.
Var.
1
1
1
1
1
0
1
2
3
4
e1
e2
e3
e4
e5
2
Observed Variables

• QoL measures at 1 year, 2 year, 3 year,
• 4 year, 5 year post-diagnosis

3
Error Terms

• ei represents time-specific variance and
• measurement error
• Procedures like regression assume there is
• no error (measures are perfectly reliable)
• LGCM explicitly models error

e1
e2
e3
e4
e5
4
Latent Intercept

• All 5 factors loadings are fixed to 1
• Mathematical trick to get the mean at
• time 1 (initial status) Var. variation of
• individual intercepts

Mean
Intercept
Var.
1
1
1
1
1
e1
e2
e3
e4
e5
5
Latent Slope

• Factors loadings (time scores) are fixed at
• 0,1,2,3,4 to represent linear growth
• Identifies the model

Mean
Slope
Var.
0
1
2
3
4
e1
e2
e3
e4
e5
6
More on fixing factor loadings for the slope
latent variable

• Why 0,1,2,3,4?
• at time 1 (y1) we have no growth (0)
• there has been a 1 year growth period at each
  subsequent time period (hence 1,2,3,4)
• this "centering" also makes the intercept factor
  interpretable
• intercept factor mean at time 1
• What if we didnt have data at the 3-year point
• factor loadings 0,1,3,4

7
More on fixing factor loadings for the slope
latent variable

• What if we had data at intake, 6 months, 12
  months, and 24 months
• time scores 0, 1, 2, 4
• What if we had a quadratic (nonlinear)
  relationship?
• create a latent variable with (squared) time
  scores
• linear 0, 1, 2, 3, 4
• quadratic 0, 1, 4, 9, 16

8
Correlation (covariance) between the latent
intercept and slope
Correlation
Mean
Mean
Intercept
Slope
Var.
Var.
1
1
1
1
1
0
1
2
3
4
e1
e2
e3
e4
e5
9
More on the correlation (covariance) between the
latent intercept and slope

• Assume the mean slope is positive
• What a positive correlation means
• individuals who have higher intercepts have
  higher slopes
• e.g., a person who starts out with high QoL will
  experience increasing QoL across time
• individuals who have lower intercepts have lower
  slopes
• e.g., a person who starts out with low QoL will
  experience smaller increases in QoL across time

10
More on the correlation (covariance) between the
latent intercept and slope

• Assume the mean slope is positive
• What a negative correlation means
• individuals who have higher intercepts have lower
  slopes
• e.g., a person who starts out with high QoL will
  experience smaller increases of QoL across time
• individuals who have lower intercepts have higher
  slopes
• e.g., a person who starts out with low QoL will
  experience greater increases in QoL across time
• Similarly when the mean slope is negative

11
Steps in conducting a LGCM

• Plot means of observed variables to determine
  general shape
• Examine variances of observed variables to get a
  sense of variation around these means
• Test an unconditional growth model
• overall model is determined as in SEM
• likelihood ratio chi-square test
• comparative fit index
• root mean-square error of approximation
• Interpret model parameters
• Test conditional models if significant residual
  variation is noted

12
Extending the LGCM model to include predictors

• If significant variation is found for the
  intercept and/or slope latent variableone can
  include predictors to explain this variation
• e.g., assume we found significant variation for
  the latent intercept variable only
• we can include group as a predictor of the latent
  intercept variable
• e.g., assume we found significant variation for
  the latent slope variable as well
• we can include group as a predictor of the latent
  slope variable as well

13
Including predictors in the LCFM model
Group
Correlation
Mean
Mean
Intercept
Slope
Var.
Var.
1
1
1
1
1
0
1
2
3
4
e1
e2
e3
e4
e5
14
Figure 12 QoL Post-Diagnosis by Group
Controls
Intervention
15
An LGCM example

• Testing an unconditional model
• 100 patients recently diagnosed with prostate
  cancer
• Qol measured on a scale from 1 to 10
• higher scores mean better QoL
• Participants are assessed once a year over a
  5-year span
• Goals include
• determine the mean trajectory of growth over time
• the variation in mean growth

16
An LGCM example

• Interpret overall model fit for linear growth
• ?2(df10)14.89, p.14, CFI.99, RMSEA.07
• Interpret Slope Parameter
• Fixed Effect
• Mean -0.621, z (CR) -8.95, p lt .001
• Random Effect (variation around the mean)
• Variance 0.357, z 5.10, p lt .001
• Interpret Intercept Parameter
• Fixed Effect (meaningful?)
• Mean 5.544, z (CR) 19.29, p lt .001
• Random Effect (variation around the mean)
• Variance 7.704, z 6.58, p lt .001

17
An LGCM example

• Interpret correlation between intercept and slope
  latent variables
• r -.794, p lt .001
• how would we interpret this in light of the
  negative slope?
• Estimated model means are estimated and can be
  plotted
• T1 5.544
• T2 4.923
• T3 4.303
• T4 3.682
• T5 3.061

18
Advanced Methods in LGCM

• Modeling accelerated/decelerated growth
• allow some time scores to be freely estimated
• you do NOT have to always fix the first 2
  time-points to 0 and 1, respectively
• but this is the general convention

19
Estimating time scores (factor loadings) to test
shape
Correlation
Mean 5.42
Mean -.411
Intercept
Slope
Var.
Var.
1
1
1
1
1



0
1
e1
e2
e3
e4
e5
20
Advanced Methods in LGCM

• Interpreting the growth curve with freely
  estimated time scores
• calculate the estimated outcome mean at each time
  point
• mean intercept (mean slope)(time score)
• t1 5.42 (-.411 0) 5.42
• t2 5.42 (-.411 1) 5.01
• t3 5.42 (-.411 2.488) 4.40
• t4 5.42 (-.411 4.584) 3.53
• t5 5.42 (-.411 5.68) 3.09
• plot these means and interpret curve

21
Growth curve based on estimated time scores at
times 3-5
22
More Advanced Methods in LGCM

• we can predict growth parameters (intercept,
  slope) with antecedent variables
• time-invariant covariates
• e.g., ethnicity, gender, personality
• time-varying covariates
• e.g., social support measures at each time-point
• we can use growth parameters to predict outcomes
  (e.g., mortality)
• we can test parallel process models
• use growth parameters to predict other growth
  parameters

23
More Advanced Methods in LGCM

• Testing for differences at specific time-points
• say we wanted to test for group differences in
  QoL at discrete time-points
• varying the center point to give the intercept
  new meaning
• altering the time scores does it
• initial status 0, 1, 2, 3, 4
• middle status -2, -1, 0, 1, 2
• final status -4, -3, -2, -1, 0
• this reparameterization does not change overall
  model fit or the slope!

24
Selected References

• Curran, P.J. (2000). A latent curve framework for
  the study of developmental trajectories in
  adolescent substance use. In J.S. Rose, L.
  Chassin, C.C. Presson, Sherman, S.S. (Eds),
  Multivariate applications in substance use
  research New methods for new questions (pp.
  1-42). Mahwah, NJ Erlbaum.
• Curran, P.J., Muthén, B.O. (1999). The
  application of latent curve analysis to testing
  developmental theories in intervention research.
  American Journal of Community Psychology, 27,
  567-595.
• Duncan, T.E., Duncan, S.C., Strycker, L.A., Li,
  F., Alpert, A. (1999). An introduction to
  latent variable growth curve modeling. Mahwah,
  NJ Erlbaum.