Normal Distributions

1
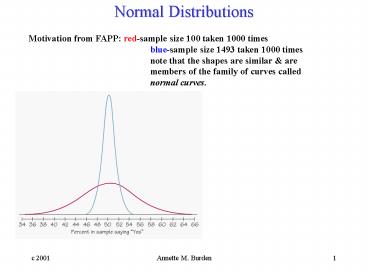
Normal Distributions
Motivation from FAPP red-sample size 100 taken
1000 times blue-sample size 1493 taken
1000 times note that the shapes are
similar are members of the family of
curves called normal curves.
2
Normal Distributions
A normal curve assigns probabilities to outcomes
as follows The probability of any interval of
outcomes is the area under the normal curve
above that interval.
3
Normal Distributions
Recall that the mean and median of a skewed
distribution are not equal. The mean lies
further toward the long tail than the
median. The mean of a normal distribution,
however, lies at the center of symmetry of the
normal curve.
Normal curves have the special property that
their spread is completely measured by a single
number, the standard deviation.
The 1st quartile mean - 0.67(s) The 3rd quartile
mean 0.67(s)
4
Normal Distributions
FAPP 68-95-99.7 Rule for Normal Distributions
5
Central Limit Theorem

• A sample mean or sample proportion from n trials
  on the same
• random phenomenon has a distribution that is
  approx normal
• when n is large.

• The mean of this normal distribution is the same
  as the mean
• for a single trial.

3. The standard deviation of this normal
distribution is the standard deviation for a
single trial divided by square root of n.
6
Application of Central Limit Theorem
Recall
7
Credits

• COMAP, For All Practical Purposes, 5th ed