Additive noise perturbation model

1
On the Lower Bound of Reconstruction Error for
Spectral Filtering Based PPDM
Songtao Guo, Xintao Wu, Yingjiu Li
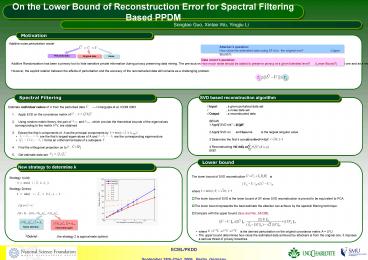
Motivation
Additive noise perturbation model
Attackers question How close the estimated
data using SF is to the original one?
(Upper Bound?)
Perturbed data
Noise
Original data
Data owners question How much noise should be
added to preserve privacy at a given tolerated
level? (Lower Bound?)
Additive Randomization has been a primary tool to
hide sensitive private information during privacy
preserving data mining. The previous work based
on Spectral Filtering empirically showed that
individual data can be separated from the
perturbed one and as a result privacy can be
seriously compromised. However, the explicit
relation between the effects of perturbation and
the accuracy of the reconstructed data still
remains as a challenging problem.
Spectral Filtering
SVD based reconstruction algorithm

• Estimate individual values of U from the
  perturbed data --- H.Kargupta et al. ICDM
  2003
• Apply EVD on the covariance matrix of
• Using random matrix theory, the pair of
  and , which provide the theoretical
  bounds of the eigenvalues corresponding to the
  matrix VTV, are obtained.
• 3. Extract the first k components of A as the
  principal components by
• are the first k largest
  eigenvalues of A and are the
  corresponding eigenvectors.
• forms an
  orthonormal basis of a subspace .
• Find the orthogonal projection on to
• Get estimate data set

Input , a given perturbed data set
, a noise data set Output
, a reconstructed data BEGIN 1 Apply SVD on
to get 2 Apply SVD on and assume
is the largest singular value 3 Determine the
first k components of by
4 Reconstructing
the data as END
Lower bound

• The lower bound of SVD reconstruction
  is
• where
• The lower bound of SVD is the lower bound of SF
  since SVD reconstruction is proved to be
  equivalent to PCA.
• The lower bound represents the best estimate the
  attacker can achieve by the spectral filtering
  technique.
• Compare with the upper bound (Guo and Wu, SAC06)
• where is
  the derived perturbation on the original
  covariance matrix A UTU.
• The upper bound determines how close the
  estimated data achieved by attackers is from the
  original one. It imposes a serious threat of
  privacy breaches

New strategy to determine k
Strategy 1(old) Strategy 2(new)
Due to , the
strategy 2 is approximate optimal.
Noise affection
Information gain
ECML/PKDD September 18th-22nd, 2006 Berlin,
Germany