Sparse matrix data structure stored by rows

1
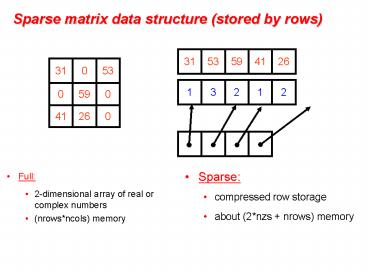
Sparse matrix data structure (stored by rows)

• Full
• 2-dimensional array of real or complex numbers
• (nrowsncols) memory

• Sparse
• compressed row storage
• about (2nzs nrows) memory

2
Distributed row sparse matrix data structure
P0
P1

• Each processor stores
• of local nonzeros
• range of local rows
• nonzeros in CSR form

P2
Pn
3
Conjugate gradient iteration to solve Axb
x0 0, r0 b, d0 r0 for k 1, 2,
3, . . . ak (rTk-1rk-1) / (dTk-1Adk-1)
step length xk xk-1 ak dk-1
approx solution rk rk-1 ak
Adk-1 residual ßk
(rTk rk) / (rTk-1rk-1) improvement dk
rk ßk dk-1
search direction

• One matrix-vector multiplication per iteration
• Two vector dot products per iteration
• Four n-vectors of working storage

4
Parallel Dense Matrix-Vector Product (Review)

• y Ax, where A is a dense matrix
• Layout
• 1D by rows
• Algorithm
• Foreach processor j
• Broadcast X(j)
• Compute A(p)x(j)
• A(i) is the n by n/p block row that processor Pi
  owns
• Algorithm uses the formula
• Y(i) A(i)X Sj A(i)X(j)

P0 P1 P2 P3
x
P0 P1 P2 P3
y
5
Matrix-vector product Parallel implementation

• Lay out matrix and vectors by rows
• y(i) sum(A(i,j)x(j))
• Skip terms with A(i,j) 0
• Algorithm
• Each processor i
• Broadcast x(i)
• Compute y(i) A(i,)x
• Optimizations reduce communication by
• Only send as much of x as necessary to each proc
• Reorder matrix for better locality by graph
  partitioning (next time)

6
Graphs and Sparse Matrices

• Sparse matrix is a representation of a (sparse)
  graph

1 2 3 4 5 6
1 1 1 2 1 1
1 3
1 1 1 4 1
1 5 1 1
6 1 1
3
2
4
1
5
6

• Matrix entries are edge weights
• Diagonal contains self-edges (usually non-zero)
• Number of nonzeros per row is the vertex degree

7
Parallel Sparse Matrix-Vector Product

• y Ax, where A is a sparse matrix
• Layout
• 1D by rows
• Algorithm
• Foreach processor j
• Broadcast X(j)
• Compute A(p)x(j)
• Same algorithm works, but
• Unbalanced if nonzeros are not evenly distributed
  over rows
• May communicate more of X than needed

P0 P1 P2 P3
x
P0 P1 P2 P3
y
8
Other memory layouts for matrix-vector product

• A column layout of the matrix eliminates the
  broadcast
• But adds a reduction to update the destination
  same total comm
• A blocked layout uses a broadcast and reduction,
  both on a subset of sqrt(p) processors less
  total comm

P0 P1 P2 P3
P0 P1 P2 P3
P4 P5 P6 P7
P8 P9 P10 P11
P12 P13 P14 P15
9
Link analysis of the web

• Web page vertex
• Link directed edge
• Link matrix Aij 1 if page i links to page j

10
Web graph PageRank (Google) Brin,
Page
An important page is one that many important
pages point to.

• Markov process follow a random link most of the
  time otherwise, go to any page at random.
• Importance stationary distribution of Markov
  process.
• Transition matrix is pA (1-p)ones(size(A)),
  scaled so each column sums to 1.
• Importance of page i is the i-th entry in the
  principal eigenvector of the transition matrix.
• But, the matrix is 8,000,000,000 by 8,000,000,000.

11
A Page Rank Matrix

• Importance ranking of web pages
• Stationary distribution of a Markov chain
• Power method matvec and vector arithmetic
• MatlabP page ranking demo (from SC03) on
  a web crawl of mit.edu (170,000 pages)