Mathematical Basis for Graphics

1
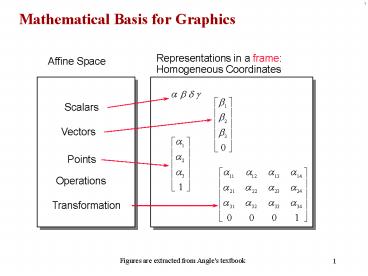
Mathematical Basis for Graphics
Representations in a frame Homogeneous
Coordinates
Affine Space
Scalars
Vectors
Points
Operations
Transformation
2
Frames and Transformations of Representations
v is representation of a point or vector in
frame
If
then
u is representation of a point or vector in
frame
is of the form
3
Instance Transformation
S
R
T
Model Coordinates
4
Important Points to Know in Matrix Definition
and Manipulation

• Matrix forms for trans, scale, rot
• Concatenation of matrices
• OpenGL commands to change matrices
• Organization of matrix data structure

5
How to Create 3D-Object Views?
6
Classical ViewingPerspective Projection
Object
COP Center of Projection origin of camera frame
Projection Plane
COP
7
Classical ViewingParallel Projection
Object

• Viewer at an infinite distance from the objects
• COP is replaced by DOP (Direction of Projection)

DOP
Projection Plane
8
Examples of Classical Views
9
Classical ViewingOrthographic Projection
10
Classical ViewingAxonometric Projections
11
Classical ViewingAxonometric Projections

• Parallel projection
• Symmetrical to principal face (PF)

General Case
Symmetric to 2PFs
Symmetric to 3 PFs
12
Dimetric Projection
13
Isometric Projection
14
Classical ViewingOblique Projection

• General case for parallel projection
• Projector can make arbitrary angle with the
  projection plan

15
Classical ViewingForeshortening
Projection Plane
Object
Object size s is foreshortened to l
u
n
q
l
s
16
Example in Parallel Projection
17
Classical ViewingPerspective Projection
How many principal directions in the object are
parallel to the projection plane?
VP2
VP1

• 3-point perspective (none)
• 2-point perspective (one)
• 1-point perspective (two)

Perspective viewing
VP3
18
Example in Perspective Projection
19
Viewing in Computer GraphicsProjection Transforms
Projection Plane
T
20
Front and Back Clipping Planes
21
OpenGLCanonical Orthographic View Volume
y
Plane z -1
Plane z 1
x
DOP
Projection Plane
z
22
Orthographic Viewing Transform
What we want
What we use
Transformation is

• Affine
• Singular

23
General OpenGlOrthographic Projection
glOrtho(xmin, xmax, ymin, ymax, zmin, zmax)
P
Canonical view volume
24
Affine Transformations for Normalization
25
General OpenGLOrthographic Projection
P
Translate View Volume
Scale View Volume
26
General OpenGLOrthographic Projection
P
Zeroed by postmult by
27
Classical ViewingPerspective Projection
Object
Projection Plane
COP
28
Perspective Projection
Parallel to the lens and orthogonal to the z-dir
More general case
3D view
Side view
Top view
29
Perspective Projection (2)
Proj. Plane
Equations are non linear. Therefore cannot use
linear affine transformation.
30
Whats problems in Perspective Projection??
All points along a projector project into the
same point, we cannot recover a point from its
projection Solution using homogeneous
coordinates to handle projections
31
Perspective Division
Consider the transformation matrix
If we allow the form
to represent a point,
we can recover the original form by division by
w. This is called perspective division.
The transformation then yields
32
Projection Pipeline
33
Canonical Perspective Transformation
34
Canonical Perspective TransformationIdea -
Transformation of View Volume
Orthographic projection is applied as last step
to project to plane z 0.
35
(No Transcript)
36
Three Steps in Determining the OpenGL Perspective
Transformation

• Shearing the window to the z-axis
• Scaling
• 3. Perspective normalization/mapping

37
Shearing Transform in 2D

• Consider shear transformation matrix along x-axis
• The term a is the proportionality constant. A
  point P (x,y,1) after transformation becomes
• Note that x is a function of y

38
Shearing Transform in 2D (cont)

• Similarly consider shear transformation matrix
  along y-axis
• The term b is the proportionality constant. A
  point P (x,y,1) after transformation becomes
• Note that y is a function of x

39
Shearing Transform in 3D

• Shear transformation matrix in (x,y) plane
• A point P (x,y,z,1) after transformation
  becomes
• Note that x and y are functions of z

40
Perspective Tx -- Shearing the window to the
z-axis

• move the ray from the origin through the window
  center onto the z axis
• when z -n, ?x should be (rl)/2n and ?y should
  be (tb)/2n, so we get 

41
Perspective Tx -- Shearing the window to the
z-axis

• So the shearing transformation will then be
• That means, the shearing matrix is given by

42
Perspective Tx --Scaling

• We want the oblique clipping planes to have
• Such that with boundaries lb-n and r t n.
• This requires a scale to make the window this
  size

43
Perspective Tx Scaling (cont)

• Therefore, the scaling matrix is given by,

44
Perspective Tx Perspective normalization/mapping

• We want to map the frustum to a 2x2x2 cube
  centered at the orgin. First, we map the bounding
  planes x ?z and y ?z to the planes x ?1 and
  y ?1. This can be done by mapping x to x/-z and
  y to y/-z

45
Perspective Tx Perspective normalization/mapping

• Ø      We use a map to homogeneous coordinates
  and then project back to 3 space by dividing
• Ø      Now, we need to solve a, b, c and d such
  that z in -n, -f maps to z in 1,1.
•  
• Ø      As x maps to x/-z, we get
•     

46
Perspective Tx Perspective normalization/mapping

• Ø      As the near plane is at z-n and the far
  plane at z-f, which map to (-1, 1) respectively,
  we get     

47
Perspective Tx Perspective normalization/mapping

• Ø  Thus, the perspective normalization matrix is
  given by,    

48
Perspective Transformation matrix

49
General OpenGL Perspective Transformation
glFrustrum(l,r,b,t,n,f)
50
Canonical Transformation of View VolumeIn OpenGL
51
General OpenGL Perspective TransformationAnother
form
gluPerspective(fovy, aspect, zNear, ZFar)
fovy Specifies the field of view angle in
degrees, in the y direction. aspect Specifies
the aspect ratio that determines the ratio of
width to height. zNear Specifies the distance
from the viewer to the near clipping plane,
always positive. zFar Specifies the distance
from the viewer to the far clipping plane, always
positive.
52
Hidden Surface Removal(Z - Buffer Algorithm)
General Approaches Object Space
Algorithms Draw back facing polygons
first. Convex objects do not render back
facing polygons. What about front facing
polygons that obstruct each other? Image Space
Algorithms Determine relationship among points
on each projector
53
Initializing Z-Buffer in OpenGL
glutInitDisplayMode(GLUT_DOUBLEGLUT_RGBGLUT_DEPT
H)
Allocates the buffer.
glEnable(GL_DEPTH_TEST)
Enables depth testing.
54
Positioning the Camera
Initially, the camera is at (0,0,0) for
perspective viewing looking in the -z
direction. To move the camera away from modeled
objects distance d along the the positive z
axis glTranslatef(0.0, 0.0, -d) What you are
really doing is translating the modeled objects
in the negative z direction. If you want to look
at the model from the positive x direction at a
distance d glTranslatef(0.0, 0.0,
-d) glRotatef(-90.0, 0.0, 1.0, 0.0)
55
A More Intuitive ApproachOffered by glu
gluLookAt(eyex, eyey, eyez, atx, aty, atz,
upx, upy, upz) eyex, eyey, eyez specify the
position of the eye point and are mapped to
the origin. atx, aty, atz specify a point being
looked at, which will be rendered in center of
view port. It is mapped to the -z axis. upx,
upy, upz specify components of the camera up
vector.