WarmUp Day 16

1
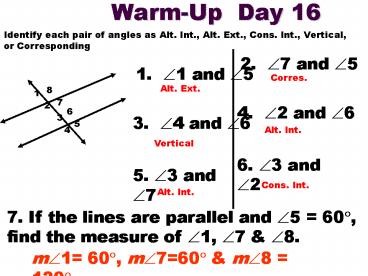
Warm-Up Day 16
Identify each pair of angles as Alt. Int., Alt.
Ext., Cons. Int., Vertical, or Corresponding
2. ?7 and ?5
1. ?1 and ?5
Corres.
Alt. Ext.
4. ?2 and ?6
3. ?4 and ?6
Alt. Int.
Vertical
6. ?3 and ?2
5. ?3 and ?7
Cons. Int.
Alt. Int.
7. If the lines are parallel and ?5 60?, find
the measure of ?1, ?7 ?8.
m?1 60?, m?760? m?8 120?.
2
Agenda
Thur 1/29 Quiz 3.1-3.4 Start 3.5

• Go over hw
• Notes 3.2 3.4
• Homework

Fri 1/30 3.6 3.7
Mon 2/2 Continue Quiz
Tues 2/3 Review Ch3
3
HW questionsP. 132 (13 problems)10 18 even,
21 26 all, 41 42

• Parallel
• skew
• 14.
• 16.
• 18. 1
• 21. corr.
• 22. alt. ext.

23. cons. int 24. alt. int. 25. alt. ext. 26.
corr. 41. B 42. C
4
HW questionsP. 146 (10 problems)8 26 even

• m?1 135? m?2 135?
• 10. m?1 82? m?2 98?
• x 71 y 109
• 14. x 65 y 115
• 16. x 130 y 130
• 18. 35
• 20. 10

22. 40 24. 23 26. 25
5
3.2 Proofs Perpendicular Lines3.4 Proving
Lines are Parallel
6
Last class.
You learned about the angles formed when two
lines are perpendicular.
7
Today, we ask.
How do we know if two lines are perpendicular?
8
Theorem 3.1
If two lines intersect to form a linear pair, of
congruent angles, then the lines are
perpendicular.
g
h
9
We have also learned
What it means to say that two angles are
complementary.
10
Today, we ask.
How do we know if two lines are complementary?
11
Theorem 3.2
If two sides of two adjacent acute angles are
perpendicular, then the angles are complementary.
12
As if that wasnt enough
We know what kind of angles are formed when two
perpendicular lines intersect.
13
Today, we ask.
How can we make this formal and use it in proofs?
14
Theorem 3.3
If two lines are perpendicular, then they
intersect to form four right angles.
15
Now lets do a proof
Given Prove ?1 and ?2 are
complementary
Page 137 Extra example 2
16
Given Prove ?1 and ?2 are
complementary
Page 137 Extra example 2
Reasons
Statements
1.
1.
BA ? BC
Given
2.
2.
?ABC is a right ?
Definition of ? lines
3.
3.
m?ABC 90?
Definition of right angle
4.
4.
m?1 m?2 m?ABC
Angle Addition Property
5.
5.
m?1 m?2 90?
Substitution Property
6.
6.
m?1 and m?2 are complementary
Definition of comp. angles
17
Last class.
You learned about special angles formed when a
transversal intersects two lines. And you
learned what happens if those two lines are
parallel.
18
If the two lines are parallel

• Corresponding angles are ?
• Alternate interior angles are ?
• Alternate exterior angles are ?
• Consecutive interior angles are supplementary

19
Today, we ask.
How do we know that two lines are parallel?
20
Alternate Interior Angles Converse Theorem
If alternate interior angles are congruent, then
the two lines are parallel.
21
Alternate Exterior Angles Converse Theorem
If alternate exterior angles are congruent, then
the two lines are parallel.
22
Consecutive Interior Angles Converse Theorem
If consecutive interior angles are supplementary,
then the two lines are parallel.
m?2 m?3 180
2
3
23
Corresponding Angles Converse Postulate
If corresponding angles are congruent, then the
two lines are parallel.
24
Two lines are Parallel if
1. A pair of corresponding ?s are ?.
2. A pair of alternate interior ?s are ?.
3. A pair of alternate exterior ?s are ?.
4. A pair of consecutive interior ?s are
supplementary.
25
Ex. 1 If m?1 5x 10 and m?2 6x 4, find x
so that ab.
m?1 m?2
5x 10 6x - 4
1
a
10 x - 4
2
14 x
b
26
Ex. 2 Identify the parallel segments.
FE CD BA
27
Ex. 3 Find the value of x so that KL MN
9x 10x - 8
-x - 8
x 8
28
Homework
P. 139 (6 problems) 11 16 P. 153 (8 problems)
10 24 even\ Quiz Tomorrow