SeriesParallel Networks

1
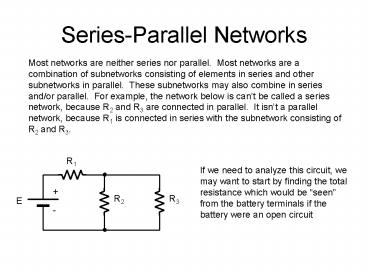
Series-Parallel Networks
Most networks are neither series nor parallel.
Most networks are a combination of subnetworks
consisting of elements in series and other
subnetworks in parallel. These subnetworks may
also combine in series and/or parallel. For
example, the network below is cant be called a
series network, because R2 and R3 are connected
in parallel. It isnt a parallel network,
because R1 is connected in series with the
subnetwork consisting of R2 and R3.
If we need to analyze this circuit, we may want
to start by finding the total resistance which
would be seen from the battery terminals if the
battery were an open circuit
2
Series-Parallel Networks
To find RT, first find the resistance of the
parallel combination of R2 and R3
RT
RT
Then add R1, which is connected in series with
the parallel combination of R2 and R3.
3
Series-Parallel Networks
After finding RT, its a simple matter to solve
for the current I1 by applying Ohms law
Next, only a portion of I1 flows through R2. The
other portion flows through R3. However, all of
I1 flows into the parallel combination, R2 R3.
We can use Ohms law to find V2
I1

V2
-
4
Series-Parallel Networks
Having found V2, which is the Voltage across R2
and also across R3, we can now find I2 and I3
I1
Weve now found all of the currents and Voltages
in the network, so its completely analyzed.

V2
-
I2
I3
5
Series-Parallel Networks
Lets see how we might find Iload in the network
below
I1
Weve now found all of the currents and Voltages
in the network, so its completely analyzed.

V2
-
I2
I3
6
Ladder Networks
There are two approaches to analyzing this
network. The first, most straightforward and
most laborious, is to find the total resistance,
RT, looking into the network (in this case, from
the battery terminals). Then use RT to find the
source current, IS. Finally, use the voltage and
current divider rules, working from the source
toward the other end of the network, to find the
branch currents and node voltages.
IS
1 W
4 W
5 W
6 W
2 W
6 W
240 V
7
Ladder Networks
R5 and R6, connected in series, may be combined
by summing their values. The equivalent is a 3 W
resistance.
IS
This 3 W resistance appears in parallel with R4.
A 3 W resistance and a 6 W resistance in parallel
combine to a single 2 W resistance
4 W
240 V
5 W
6 W
3 W
6 W
IS
4 W
240 V
5 W
2 W
6 W
8
Ladder Networks
This 2 W resistance is in series with R3, and
those two resistors add up to a 6 W equivalent
resistance
IS
Now we see two 6 W resistors in parallel, These
combine to an equivalent resistance of 3 W
240 V
5 W
6 W
6 W
IS
30 A
The total resistance seen by the 240 V source is
a 5 W resistor in series with a 3 W resistor, or
8 W. Is is given by
240 V
5 W
3 W
9
Ladder Networks
Now we know that the source current, Is, is 30 A.
The Voltage drop across R1 is given by
90 V
IS
30 A
Subtracting this from the source voltage, we
finde that the Voltage at the node shown is 90
V. The 3 W resistor is actually the equivalent of
R2 in parallel with another 6 W resistor. The
second resistor is the equivalent of all elements
to the right of R2. Ohms law tells us the
current through R2 is 15 A, so 15 A continues to
the right.
240 V
5 W
3 W
90 V
15 A
IS
240 V
5 W
15 A
6 W
6 W
10
Ladder Networks
The second 6 W resistance is actually the series
combination of R3, a 4 W resistor, with the 2 W
equivalent of everything to the right of R3.
4 W
30 V
90 V
30 A
IS
The 2 W equivalent resistance is actually the 6 W
of R4 in parallel with the 3 W equivalent of
everything to the right of R4. The current
divider rule tells us the current through R4 is
240 V
5 W
15 A
15 A
2 W
6 W
90 V
IS
30 V
30 A
4 W
240 V
5 W
15 A
5 A
10 A
This leaves 10 A to continue to the right.
15 A
6 W
3 W
6 W
11
Ladder Networks
The 3 W resistance is actually the series
combination of R5 and R6, so the current through
both of these is 10 A. Ohms law shows that the
Voltage across R6 is 20 V. This completes the
analysis of this ladder network.
30 V
IS
90 V
1 W
30 A
20 V
4 W
5 W
15 A
5 A
10 A
15 A
6 W
2 W
6 W
240 V
12
Ladder Networks
Lets back up and take another look at the ladder
network. First, recall that everything to the
right of R2 could be represented by a 6 W
resistor as shown below. We dont need to know
the value of Is to know that it divides evenly
between the two paths.
Next, apply KVL around the loop consisting of E,
R1 and R2
Is/2
IS
240 V
5 W
Is/2
6 W
6 W
The current through R2 is 15 A, so the Voltage
across R2 is 90 V.
13
Ladder Networks
Of the 30 A flowing through R1, 15 A returns to
the source via R2 and 15 A flows through R3. The
current flowing through R3 enters another current
divider. 1/3, or 5A, flows through R4 the
remaining 10 A flows through the 3 W equivalent
resistance.
The Voltage drop across R4 is 30 V. This is the
Voltage at the indicated node.
90 V
IS
30 V
30 A
4 W
240 V
5 W
15 A
5 A
10 A
15 A
6 W
3 W
6 W
14
Ladder Networks
The 3 W resistance is actually the series
combination of R5 and R6, so the current through
both of these is 10 A. Ohms law shows that the
Voltage across R6 is 20 V. This again completes
the analysis of this ladder network.
30 V
IS
90 V
1 W
30 A
20 V
4 W
5 W
15 A
5 A
10 A
15 A
6 W
2 W
6 W
240 V
15
R-2R Ladder
This is a special type of ladder network, called
an R-2R ladder.
The two 2R resistors in parallel at the right end
can be combined into a single resistor R
16
R-2R Ladder
The two Rs at the right end are in series, and
combine to a single 2R
Again, the two 2R resistors in parallel at the
right end can be combined into a single resistor R
17
R-2R Ladder
The current I entering the network divides evenly
at the first node
I
And then it divides evenly again. An N-rung R-2R
ladder divides the current by half at each rung.
I
18
R-2R Ladder
Heres an application for an R-2R ladder.
Applying KVL to the loop formed by ground, E and
the first two reisistors,
E
I
1
1
1
0
0
0

-
19
R-2R Ladder
The position of the switches doesnt change the
current flowing in any of the 2R resistors only
where it goes. With all three switches in the
1 position, all of the current flows through
the feedback resistor.
E
I
1
1
1
0
0
0

Vout
0 V
-
20
R-2R Ladder
Notice that the switches are set at binary 7
E
I
1
1
1
0
0
0

Vout
0 V
-
21
R-2R Ladder
If the switches were set to binary 5
E
I
1
1
1
0
0
0

Vout
0 V
-
22
R-2R Ladder
If the switches were set to binary n,
E
I
1
1
1
0
0
0

Vout
0 V
-
23
R-2R Ladder
This circuit is a 3-bit analog-to-digital
converter. The binary number represented by the
switch setting is converted to an analog Voltage.
The resolution can be increased to M bits by
adding rungs to the ladder.
E
I
1
1
1
0
0
0

Vout
0 V
-
24
Bridge Network
Heres a bridge network. The bridge consists of
R1, R2, R3 and R4, and the bridge is balanced if
the current through Rload is zero.

E
-
25
Bridge Network
When the bridge is balanced, zero current flows
through Rload. For zero current to flow through
the load, the voltage across the load must be
zero, so we might just as well remove the load.
For Vload to be zero, Va and Vb must be equal.
If we treat the bridge network as two Voltage
dividers, one consisting of R1 and R2 and the
other of R3 and R4,
Vload

E
-
Va

Vb
-
26
Bridge Network
So,
Vload

E
-
Va

Vb
-
So, for the bridge to be balanced,
27
Bridge Network
If the bridge is unbalanced and loaded, the
problem is considerably more complex. We cant
simplify the circuit by combining resistors,
because no two resistors are connected either in
series or parallel.
Lets try analyzing the circuit by finding its
Thevenin equivalent, from Rloads viewpoint.

E
-
28
Bridge Network
First, lets find Eth by removing Rload and
calculating the open-circuit Voltage across the
terminals from which Rload was removed
Vb
Vload

E

-
Va
Vc
-
29
Bridge Network
Vb
Vload

E

-
Va
Vc
-
30
Bridge Network
Vb
Vload

E

-
Va
Vc
-
31
Bridge Network
Vb
Vload

E

-
Va
Vc
-
32
Bridge Network
Vb
Note If you plug the resistance values given in
Example 11-11, you get
Vload

E

-
Va
Vc
-
33
Bridge Network
Next, short-circuit the load terminals and
calculate the short-circuit current.
Vb
Isc

E
Va
Vc
-
34
Bridge Network
Next, short-circuit the load terminals and
calculate the short-circuit current.
Vb
Is
Isc

E
Va
Vc
-
35
Bridge Network
Next, short-circuit the load terminals and
calculate the short-circuit current.
Vb
Is
I1
I3
Isc

E
Va
Vc
-
I2
36
Bridge Network
Next, short-circuit the load terminals and
calculate the short-circuit current.
Vb
Is
I1
I3
Isc

E
Va
Vc
-
I2
37
Bridge Network
Vb
Is
I1
I3
Isc

E
Va
Vc
-
I2
38
Bridge Network
Now, find the Thevenin resistance by dividing ETh
by Isc
Iload

Vload

ETh
-