Gravitational Potential Energy

1
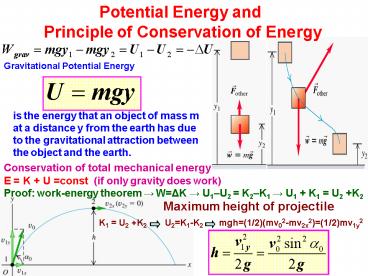
Potential Energy and Principle of Conservation
of Energy
Gravitational Potential Energy
is the energy that an object of mass m at a
distance y from the earth has due to the
gravitational attraction between the object and
the earth.
Conservation of total mechanical energy E K U
const (if only gravity does work) Proof
work-energy theorem ? W?K ? U1U2 K2K1 ? U1
K1 U2 K2
Maximum height of projectile
K1 U2 K2 U2K1-K2
mgh(1/2)(mv02-mv2x2)(1/2)mv1y2
2
Exam Example 14 Riding loop-the-loop (problem
7.46)
Data R 20 m, v00, m100 kg
Find (a) min h such that a car does not fall
off at point B, (b) kinetic energies for that
hmin at the points B, C, and D, (c) if h 3.5
R, compute velocity and acceleration at C.
D
Solution

• To avoid falling off, centripetal acceleration
  v2/R g ? v2 gR.
• Conservation of energy KB2mgRmgh ?
  (1/2)mvB2mg(h-2R) .
• Thus, 2g(h-2R) gR ? h 5R/2 , that is
  hmin 5R/2.
• KfUfK0U0 , K00 ? KB mghmin- 2mgR
  mgR/2 ,
• KC mghmin- mgR 3mgR/2 , KD
  mghmin 5mgR/2.
• (c) (1/2)mvC2 KC mgh mgR 2.5 mgR ? vC
  (5gR)1/2
• arad vC2/R 5g, atan g since the only
  downward force is gravity.

3
Elastic Potential Energy
Fx -kx
Conservation of total mechanical energy E K U
const (if only elastic force does work)
Proof work-energy theorem ? W?K ?
U1 U2 K2 K1 ? U1 K1 U2 K2
Conservation of total mechanical energy when
gravitational and elastic forces do work
0
4
Conservative and Nonconservative Forces
Two equivalent definitions of conservative
forces A force is conservative when
(Version 1) when the work it does on a moving
object is independent of the path (W2 W1) ,
or (Version 2) when it does no net work on an
object moving around a closed path ( W2 W1 0
) .
2
1
General concept of potential energy
Conservative forces gravitational force, elastic
spring force, electric force.
Nonconservative forces are irreversible
static and kinetic friction forces, air
resistance, any dissipative forces,
tension, normal force, propulsion force of
a rocket.
Important Potential energy is not defined for a
nonconservative force !
5
Conservative Force is a Gradient of Potential
Energy
6
Energy Diagrams and Oscillations in a Potential
Well
Ugrav mgy
7
Work-Energy Theorem in Terms of Conservative and
Nonconservative Forces
Definition of the total mechanical energy E K
U
Work-Energy Theorem E E0 Wnc
Any change in the total mechanical energy of an
object is entirely due to the work done by
external nonconservative forces.
Typical examples 1. Friction and
resistance irreversibly decrease the total
mechanical energy
Wnc - fks increases the total mechanical energy
Wnc Fs 0 ? E E0
The Principle of Conservation of Mechanical
Energy K U const if Wnc 0
8
The Principle of Conservation of Energy
Work-Energy Theorem ? ?K ?U Wother Let us
introduce an internal energy so that ?Eint -
Wother , then ?K ?U ?Eint 0 , i.e., there
is no missing energy !
K U Eint Etotal const Energy can neither
be created nor destroyed, but can only be
converted from one form to another.
Forms of Energy kinetic energy, gravitational
energy, energy of electromagnetic fields
(electric energy and magnetic energy), heat
(thermal energy), chemical energy, nuclear
energy,
Nuclear fission U235 n ? A1 A2 2n 200
MeV , 1 eV 1.610-19 J
Nuclear fusion ITER (tokomak reactor) 1D2 1T3
? 2He4 n 17 MeV
p-p cycle in stars 4p ? 2He4 25 MeV
He3 D ? He4 p 18 MeV
(thermonuclear reactions).
Einsteins equation E0 mc2 ? Mass is
equivalent to energy !
mec2 910-31 kg (3108 m/s)2 10-13 J 0.5
MeV annihilation e- e ? 2?
Energy of the sun is finite! Esun Msun c2
21030 kg (3108 m/s)2 21047 J
9
Exam Example 15 Spring on the Incline (problem
7.74)
Data m 2 kg, ? 53.1o, y0 4 m, k 120 N/m,
µk 0.2, v0 0.

• Find (a) kinetic energy and speed at the 1st and
  2nd passages of y0,
• the lowest position ys and friction energy losses
  on a way to ys,
• (c) the highest position yf after rebound.

y
m
Solution work-energy theorem Wnc?K?Ugrav?Uel
y0

• 1st passage Wnc -y0µkmg cos? since fkµkFN
• µkmg cos?, ?KK1 , ?Ugrav - mgy0 sin?, ?Uel0
• ? K1mgy0(sin?-µkcos?),
• v1(2K1/m)1/2 2gy0(sin?µkcos?)1/2
• 2nd passage Wnc - (y02ys) µkmg cos?, ?KK2,
  
• ?Ugrav -mgy0sin?, ?Uel0 ?
• K2mgy0sin?-(y02ys) µkmgcos?, v2(2K2/m)1/2

yf
0
ys
?
(b) (1/2)kys2 Uel ?Uel Wnc ?Ugrav mg
(y0ys) (sin?-µkcos?) ? ays2 ys y0 0, where
ak/2mg (sin?-µkcos?), ? ys -1 -
(14ay0)1/2/(2a) Wnc - (y0ys)
mgµkcos?
(c) Kf 0, ?Uel0, ?Ugrav -(y0yf) mg sin?, Wnc
-(y0yf2ys) µkmg cos? ?