Graphs

1
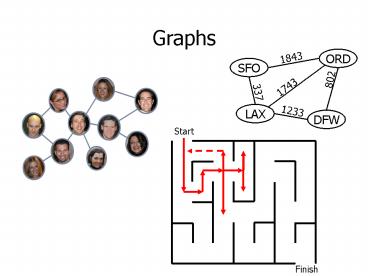
Graphs
Start
Finish
2
(No Transcript)
3
Friends
Sally
Barbara
Bob
Joe
Carl
Jim
Mary
Steve
Jane
Karen
4
Road System
5
Graph

• A graph is a pair (V, E), where
• V is a set of nodes, called vertices
• E is a collection of pairs of vertices, called
  edges
• An Edge is a pair of elements from V
• (SFO, LAX) and (DFW, MIA) are elements of E
• (HNL, SFO) is not an element of E

6
Undirected Edges
7
Directed Edges
8
Edge Types

• Directed edge
• ordered pair of vertices (u,v)
• first vertex u is the origin
• second vertex v is the destination
• ex a flight
• Undirected edge
• unordered pair of vertices (u,v)
• ex airways route or two-way street

9
Directed graph

• All the edges are directed
• Ex We-Fly-Cheap Airlines flight schedule

PVD
ORD
SFO
WFC 2245
LGA
WFC 3475
HNL
LAX
WFC 4657
WFC 2112
DFW
MIA
10
Undirected Graph

• All the edges are undirected
• Ex Airways routes (typically undirected)
• Mixed graph

J35
PVD
ORD
J2
SFO
J29
LGA
J35
J56
HNL
LAX
J36
DFW
J36
MIA
J36
11
Graph Terminology

• End vertices (or endpoints) of an edge
• Edges incident on a vertex
• Adjacent vertices
• Degree of a vertex
• In-degree
• Out-degree

12
More Graph Terminology

• Parallel edges
• Self-loop
• Simple graph

13
Graph Properties

• Property 1
• Property 2
• In a directed graph G
• Property 3
• In a simple directed graph
• m ? n (n - 1)
• Property 4
• In a simple undirected graph
• m ? n (n - 1)/2

Given Graph G (V, E) where n number of
vertices m number of edges deg(v) is the degree
of vertex v
14
Some More Terminology

• Path
• A sequence of vertices and edges that
• start at a vertex
• end with a vertex
• each edge is incident to its predecessor and
  successor in sequence
• Directed Path
• A path that follows directed edges
• Simple path
• A path such that all its vertices and edges are
  distinct

15
And More

• Cycle
• Directed cycle
• Acyclic
• Subgraph of G (V, E)
• Spanning subgraph of G

16
And Still More Terminologyplease make it stop!

• Connected
• Spanning Tree of G

17
Graph ADT

• Accessor methods
• endVertices(e)
• opposite(v, e)
• areAdjacent(v, w)
• connectingEdge(v, w)
• Update methods
• insertVertex(x)
• insertEdge(v, w, l)
• removeVertex(v)
• removeEdge(e)
• Iterator methods
• incidentEdges(v)
• vertices()
• edges()

18
Representing Graphs

• Adjacency lists
• Adjacency matrices

19
Searching

• Generic way to visited the vertices of a graph
• Generic
• Depth First
• Breadth First
• Shortest Path (Dijkstras Algorithm)

20
Searching

• findPath(G, v, u)
• Container c
• v.prev null
• v.visited true
• c.insert(v)
• while (!c.isEmpty() (v c.remove())! u)
• for each e in G.incidentEdges(v)
• w G.opposite(v, e)
• if (!visited(w))
• w.visited true
• w.prev v
• c.insert(w)
• if (v u)
• return reconstructPath(v)
• else
• return null

21
Path Reconstruction

• reconstructPath(G, v)
• list s
• while (v.prev ! null)
• s.insertAtFront(v)
• s.insertAtFront(G.connectingEdge(v, v.prev)
• v v.prev

22
Depth First Search

• dfs(G)
• for each v in G.vertices()
• if (!v.visited)
• dfs(G, v)
• dfs(G, v)
• v.visited true
• for each e in G.incidentEdges(v)
• w v.opposite(v, e)
• if (!w.visited)
• w.visited true
• dfs(G, w)

23
Directed Graphs

• A digraph is a graph whose edges are all directed
• Short for directed graph
• Applications
• one-way streets
• flights
• task scheduling

24
Reachability

• DFS tree rooted at a vertex v vertices reachable
  from v via directed paths

E
D
C
F
A
B
25
Strong Connectivity

• Each vertex can reach all other vertices

26
Testing For Strong Connectivity

• Pick a vertex v in G.
• Perform a DFS from v in G.
• If theres a w not visited, then no.
• Let G be G with edges reversed.
• Perform a DFS from v in G.
• If theres a w not visited, then no.
• Else, yes.
• Running time O(nm)

27
Weighted Graphs

• In a weighted graph, each edge has an associated
  numerical value, called the weight of the edge
• Edge weights may represent, distances, costs,
  time, etc.
• Example
• In a flight route graph, the weight of an edge
  represents the distance in miles between the
  endpoint airports

28
Shortest Paths

• Given a weighted graph and two vertices u and v,
  we want to find a path of minimum total weight
  between u and v.
• The length of a path is the sum of the weights
  of its edges.
• The distance from u to v, denoted d(u,v) is the
  length of the minimum length path, or the
  shortest path.
• Example
• Shortest path between Providence and Honolulu
• d(PVD, HNL) 5,147

29
Dijkstras Algorithm

• Single source, positive weight shortest path
  algorithm
• Can be used on directed or undirected graphs
• Assumes all edge weights are 0
• Greedy algorithm that perform a weighted
  Breadth First Search of the graph
• Uses a priority queue as the container
• always adds the minimum weighted vertex as the
  next vertex in its shortest path
• relaxes edges to update path lengths

30
Edge Relaxation

• Consider an edge e (u,z) such that
• u is the vertex most recently added to the
  shortest path
• z has not been added to the path
• The relaxation of edge e updates distance d(z) as
  follows
• d(z) ? mind(z),d(u) weight(e)
• In other words, if using edge e allows us to
  reach z in a shorter distance, then we add e to
  our edges and update zs distance
• d(z) d(u) weight(e)

d(u) 50
d(z) 75
10
e
u
z
s

d(u) 50
d(z) 60
10
e
u
z
s

31
Example

• Find the shortest paths from s to all other
  vertices

w
z
1
?
?
10
2
3
9
s
6
4
0
7
5
?
?
2
y
x
32
Example Continued
w
w
z
z
1
1
10
?
10
?
10
10
2
2
3
3
9
9
s
s
6
4
6
4
0
0
7
7
5
5
5
?
5
?
2
2
y
y
x
x
w
z
w
z
1
1
8
14
8
14
10
10
2
3
2
3
9
9
s
s
6
4
6
0
4
0
7
7
5
5
5
7
5
7
2
2
y
y
x
x
33
Example Continued
w
z
w
z
1
8
13
1
10
8
13
10
2
3
9
s
6
4
2
0
3
9
s
6
4
0
7
7
5
5
7
5
2
5
7
y
2
x
y
x
z
w
w
z
1
1
8
9
8
9
10
10
2
3
9
2
3
9
s
6
4
s
0
6
4
0
7
7
5
5
5
7
5
7
2
2
y
x
y
x
34
Dijkstras Algorithm(Single Source to All
Vertices)

• Dijkstra (G, v)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()))
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

Edge relaxation
35
Whats the Running Time ofDijkstras Algorithm?
It depends on the implementation of the Priority
Queue!
OK, so whats the best implementation?

• Dijkstra (G, v)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()))
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

It depends on how dense or sparse your graph
is!
36
Heap Implementation
Every vertex will eventually be examined, so the
while-loop will run once for each vertex in the
graph (v?G)

• Dijkstra (G, v)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()))
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

log n
deg(v) edges
log n
log n
37
Heap Implementation
changeKey or insert
while-loop
removeMin
IncidentEdges
From Property 1
38
Unsorted List Implementation
Every vertex will eventually be examined, so the
while-loop will run once for each vertex in the
graph (v?G)

• Dijkstra (G, v)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()))
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

n
deg(v) edges
1
1
39
Unsorted List Implementation
changeKey or insert
while-loop
removeMin
IncidentEdges
From Property 1
40
So which is faster, heap or unsorted list?
When the graph is dense, mO(n2), therefore heap
O((mn) logn) O((n2 n) logn) heap
O(n2logn) list O(n2) When the graph is
sparse, mO(n), therefore heap O((mn)
logn) O((n n) logn) heap
O(nlogn) list O(n2)
The unsorted list is faster when the graph is
dense!
The heap is faster when the graph is sparse!
41
Dijkstras AlgorithmSingle Source to Single
Destination Vertex

• Dijkstra (G, v, u)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()) !
  u)
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

42
Dijkstras Algorithm

• Dijkstra (G, v, u)
• v.prev null
• v.dist 0
• v.visited true
• PriorityQueue c new PriorityQueue
• c.insert(v.dist, v)
• while((!c.isEmpty()) (p c.removeMin()) !
  u)
• for each edge e in G.incidentEdges(p)
• w G.opposite(p, e)
• if (w.visited)
• if ((p.dist e.cost) lt w.dist)
• w.prev p
• w.dist p.dist e.cost
• c.changeKey(w.dist, w)
• else if (!w.visited)
• w.prev p
• w.visited true
• w.dist p.dist e.cost
• c.insert(w.dist, w)

43
Minimum Spanning Trees

• Kruskals Algorithm
• Prims Algorithm

44
Kruskals Algorithm

• Kruskal (G)
• Q new PriorityQueue()
• for each v ? G do
• Create container c(v) v
• initialize Q with edges of G using weight as key
• Tree MST new Tree()
• while MST has fewer than n-1 edges
• edge (u, v) Q.removeMin()
• let c(u) and c(v) be the clusters containing u
  v
• if ( c(v) ? c(u) )
• Add edge (u, v) to T
• Merge c(u) and c(v) into a single cluster
• Return MST

45
(No Transcript)
46
Prims Algorithm

• Prim(G)
• pick starting vertex v
• v.dist 0
• v.prev null
• for each vertex u ? v in G
• u.dist 8
• Tree MST new Tree()
• initialize Q with vertices of G using distance
  as key
• while (!Q.isEmpty())
• Vertex u Q.removeMin()
• MST.insert(u)
• for each edge e in G.incidentEdges(u)
• w G.opposite(u, e)
• if (!MST.contains(w))
• if ((u.dist e.cost) lt w.dist)
• w.dist u.dist e.cost
• c.changeKey(w.dist, w)
• prev u
• return MST

47
(No Transcript)