Atomic Structure

1
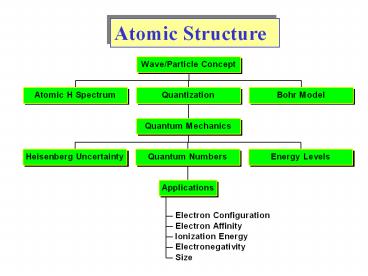
Atomic Structure
2
Wave-Particle Duality
3
The Wave Nature of Light

• All waves have a characteristic wavelength, l,
  and amplitude, A.
• Frequency, n, of a wave is the number of cycles
  which pass a point in one second.
• Speed of a wave, c, is given by its frequency
  multiplied by its wavelength
• For light, speed c 3.00x108 m s-1 .
• The speed of light is constant!
• Higher Quality video (230 sec into video).

4
The Wave Nature of Light
5
The Wave Nature of Light
6
The Wave Nature of Light
7
(No Transcript)
8
(No Transcript)
9
Quantized Energy and Photons

• Planck energy can only be absorbed or released
  from atoms in certain amounts called quanta.
• The relationship between energy and frequency is
• where h is Plancks constant ( 6.626 ? 10-34 J s
  ) .

10
Quantized Energy and Photons

• The Photoelectric Effect and Photons
• Einstein assumed that light traveled in energy
  packets called photons.
• The energy of one photon is

11
Nature of Waves Quantized Energy and Photons
12
Line Spectra and the Bohr Model

• Line Spectra
• Radiation composed of only one wavelength is
  called monochromatic.
• Radiation that spans a whole array of different
  wavelengths is called continuous.
• White light can be separated into a continuous
  spectrum of colors.
• Note that there are no dark spots on the
  continuous spectrum that would correspond to
  different lines.

13
(No Transcript)
14
Line Spectra and the Bohr Model

• Bohr Model
• Colors from excited gases arise because electrons
  move between energy states in the atom.
  (Electronic Transition)

15
(No Transcript)
16
Line Spectra and the Bohr Model

• Bohr Model
• Since the energy states are quantized, the light
  emitted from excited atoms must be quantized and
  appear as line spectra.
• After lots of math, Bohr showed that
• where n is the principal quantum number (i.e., n
  1, 2, 3, and nothing else).

17
Line Spectra and the Bohr Model

• Bohr Model
• We can show that
• When ni gt nf, energy is emitted.
• When nf gt ni, energy is absorbed

18
Line Spectra and the Bohr Model
Bohr Model
Mathcad (Balmer Series)
CyberChem (Fireworks) video
19
Line Spectra and the Bohr Model Balmer Series
Calculations
20
(No Transcript)
21
Line Spectra and the Bohr Model Balmer Series
Calculations
22
Line Spectra and the Bohr Model

• Limitations of the Bohr Model
• Can only explain the line spectrum of hydrogen
  adequately.
• Can only work for (at least) one electron atoms.
• Cannot explain multi-lines with each color.
• Electrons are not completely described as small
  particles.
• Electrons can have both wave and particle
  properties.

23
The Wave Behavior of Matter

• Knowing that light has a particle nature, it
  seems reasonable to ask if matter has a wave
  nature.
• Using Einsteins and Plancks equations, de
  Broglie showed
• The momentum, mv, is a particle property, whereas
  ? is a wave property.
• de Broglie summarized the concepts of waves and
  particles, with noticeable effects if the objects
  are small.

24
The Wave Behavior of Matter

• The Uncertainty Principle
• Heisenbergs Uncertainty Principle on the mass
  scale of atomic particles, we cannot determine
  exactly the position, direction of motion, and
  speed simultaneously.
• For electrons we cannot determine their momentum
  and position simultaneously.
• If Dx is the uncertainty in position and Dmv is
  the uncertainty in momentum, then

25
Energy and Matter
E m c2
26
Quantum Mechanics and Atomic Orbitals

• Schrödinger proposed an equation that contains
  both wave and particle terms.
• Solving the equation leads to wave functions.
• The wave function gives the shape of the
  electronic orbital. Shape really refers to
  density of electronic charges.
• The square of the wave function, gives the
  probability of finding the electron ( electron
  density ).

27
Quantum Mechanics and Atomic Orbitals
Solving Schrodingers Equation gives rise to
Orbitals. These orbitals provide the electron
density distributed about the nucleus. Orbitals
are described by quantum numbers.
Sledge-O-Matic- Analogy
28
Quantum Mechanics and Atomic Orbitals

• Orbitals and Quantum Numbers
• Schrödingers equation requires 3 quantum
  numbers
• Principal Quantum Number, n. This is the same as
  Bohrs n. As n becomes larger, the atom becomes
  larger and the electron is further from the
  nucleus. ( n 1 , 2 , 3 , 4 , . )
• Angular Momentum Quantum Number, ?. This quantum
  number depends on the value of n. The values of
  ? begin at 0 and increase to (n - 1). We usually
  use letters for ? (s, p, d and f for ? 0, 1,
  2, and 3). Usually we refer to the s, p, d and
  f-orbitals.
• Magnetic Quantum Number, m?. This quantum number
  depends on ? . The magnetic quantum number has
  integral values between - ? and ? . Magnetic
  quantum numbers give the 3D orientation of each
  orbital.

29
Quantum Numbers of Wavefuntions
30
Quantum Mechanics and Atomic Orbitals
31
Quantum Mechanics and Atomic Orbitals

• Orbitals and Quantum Numbers

32
Representations of Orbitals
The s-Orbitals
33
Representations of Orbitals
The p-Orbitals
34
d-orbitals
35
Orbitals and Their Energies
Orbitals CD
Many-Electron Atoms
36
Many-Electron Atoms
Electron Spin and the Pauli Exclusion Principle
37
Many-Electron Atoms

• Electron Spin and the Pauli Exclusion Principle
• Since electron spin is quantized, we define ms
  spin quantum number ? ½.
• Paulis Exclusions Principle no two electrons
  can have the same set of 4 quantum numbers.
• Therefore, two electrons in the same orbital must
  have opposite spins.

38
Figure 6.27
Orbitals CD
39
Orbitals CD
Figure 6.28
40
Orbitals and Their Energies
Orbitals CD
Many-Electron Atoms
41
Electron Configurations
42
Electron Configurations
43
Metals, Nonmetals, and Metalloids
Metals
Figure 7.14
44
Periodic Trends

• Two Major Factors
• principal quantum number, n, and
• the effective nuclear charge, Zeff.

45
Figure 7.5 Radius video Clip
46
Figure 7.6
47
Figure 7.10 IE clip
48
Figure 7.9
49
Electron Affinities

• Electron affinity is the opposite of ionization
  energy.
• Electron affinity the energy change when a
  gaseous atom gains an electron to form a gaseous
  ion
• Cl(g) e- ? Cl-(g)
• Electron affinity can either be exothermic (as
  the above example) or endothermic
• Ar(g) e- ? Ar-(g)

50
Figure 7.11 Electron Affinities
51
Group Trends for the Active Metals
Group 1A The Alkali Metals
52
Group Trends for the Active Metals
Group 2A The Alkaline Earth Metals
53
Group Trends for Selected Nonmetals
Group 6A The Oxygen Group
54
Group Trends for Selected Nonmetals
Group 7A The Halogens
55
Group Trends for the Active Metals

• Group 1A The Alkali Metals
• Alkali metals are all soft.
• Chemistry dominated by the loss of their single s
  electron
• M ? M e-
• Reactivity increases as we move down the group.
• Alkali metals react with water to form MOH and
  hydrogen gas
• 2M(s) 2H2O(l) ? 2MOH(aq) H2(g)

56
Group Trends for the Active Metals

• Group 2A The Alkaline Earth Metals
• Alkaline earth metals are harder and more dense
  than the alkali metals.
• The chemistry is dominated by the loss of two s
  electrons
• M ? M2 2e-.
• Mg(s) Cl2(g) ? MgCl2(s)
• 2Mg(s) O2(g) ? 2MgO(s)
• Be does not react with water. Mg will only react
  with steam. Ca onwards
• Ca(s) 2H2O(l) ? Ca(OH)2(aq) H2(g)

57
Atomic Structure