Picturing Location and Spread with Boxplots

1
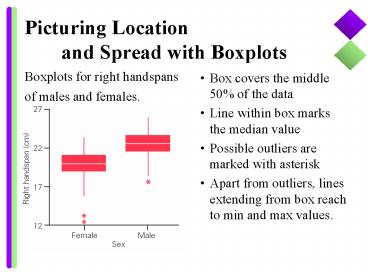
Picturing Location and Spread with Boxplots
Boxplots for right handspans of males and
females.

• Box covers the middle 50 of the data
• Line within box marks the median value
• Possible outliers are marked with asterisk
• Apart from outliers, lines extending from box
  reach to min and max values.

2
How to Draw a Boxplot of a Quantitative Variable
Step 1 Label either a vertical axis or a
horizontal axis with numbers from min to max of
the data. Step 2 Draw box with lower end at Q1 a
nd upper end at Q3. Step 3 Draw a line through t
he box at the median M. Step 4 Draw a line from
Q1 end of box to smallest data value that is not
further than 1.5 ? IQR from Q1. Draw a line from
Q3 end of box to largest data value that is not
further than 1.5 ? IQR from Q3.
Step 5 Mark data points further than 1.5 ? IQR
from either edge of the box with an asterisk.
Points represented with asterisks are considered
to be outliers.
3
2.7 Bell-Shaped Distributions of Numbers

• Many measurements follow a predictable pattern
• Most individuals are clumped around the center
• The greater the distance a value is from the
  center, the fewer individuals have that value.

Variables that follow such a pattern are said to
be bell-shaped. A special case is called a
normal distribution or normal curve.
4
Example 2.11 Bell-Shaped British Womens
Heights

• Data representative sample of 199 married
  British couples.Below shows a histogram of the
  wives heights with a normal curve superimposed.
  The mean height 1602 millimeters.

5
Describing Spread with Standard Deviation
Standard deviation measures variability by
summarizing how far individual data values are
from the mean. Think of the standard deviation
as roughly the average distance values fall from
the mean.
6
Describing Spread with Standard Deviation
Both sets have same mean of 100.
Set 1 all values are equal to the mean so there
is no variability at all. Set 2 one value equal
s the mean and other four values are 10 points
away from the mean, so the average distance away
from the mean is about 10.
7
Calculating the Standard Deviation
Formula for the (sample) standard deviation
The value of s2 is called the (sample) varia
nce. An equivalent formula, easier to compute,
is
8
Calculating the Standard Deviation
Step 1 Calculate , the sample mean.
Step 2 For each observation, calculate the
difference between the data value and the mean.
Step 3 Square each difference in step 2.
Step 4 Sum the squared differences in step 3,
and then divide this sum by n 1.
Step 5 Take the square root of the value in
step 4.
9
Calculating the Standard Deviation
Consider four pulse rates 62, 68, 74, 76
Step 1
Steps 2 and 3
Step 4
Step 5
10
Population Standard Deviation
Data sets usually represent a sample from a
larger population. If the data set includes
measurements for an entire population, the
notations for the mean and standard deviation are
different, and the formula for the standard
deviation is also slightly different. A
population mean is represented by the symbol m
(mu), and the population standard deviation is
11
Interpreting the Standard Deviation for
Bell-Shaped Curves The Empirical Rule

• For any bell-shaped curve, approximately
• 68 of the values fall within 1 standard
  deviation of the mean in either direction
  
• 95 of the values fall within 2 standard
  deviations of the mean in either direction
  
• 99.7 of the values fall within 3 standard
  deviations of the mean in either direction

12
The Empirical Rule, the Standard Deviation, and
the Range

• Empirical Rule the range from the minimum to
  the maximum data values equals about 4 to 6
  standard deviations for data with an approximate
  bell shape.
• You can get a rough idea of the value of the
  standard deviation by dividing the range by 6.

13
Standardized z-Scores
Standardized score or z-score
Example Mean resting pulse rate for adult men
is 70 beats per minute (bpm), standard deviation
is 8 bpm. The standardized score for a resting
pulse rate of 80
A pulse rate of 80 is 1.25 standard deviations
above the mean pulse rate for adult men.
14
The Empirical Rule Restated

• For bell-shaped data,
• About 68 of the values have z-scores between
  1 and 1.
  
• About 95 of the values have z-scores between
  2 and 2.
  
• About 99.7 of the values have z-scores between
  3 and 3.