DoubleSlit Interference: Schematic

1
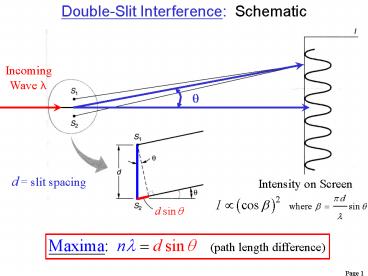
Double-Slit Interference Schematic
Incoming Wave l
q
d slit spacing
Intensity on Screen
2
Photons Wave-like Behavior

• de Broglie (1924) proposed that ALL particles
  (photon, electron, atoms, etc.) have an
  associated wavelength l h/p.
• Proof for photon (zero mass) given by

Rest mass
From Relativity
For a Photon (m 0)
3
Momentum and Energy Get it Right!

• Momentum and Energy DEFINITIONS

• Energy vs. Momentum RELATIONSHIPS

4
Electrons Wave-like Behavior

• Every particle has a wavelength given by
• Question Why are there no observed effects of
  particle waves (i.e., diffraction and
  interference) in day-to-day life?
• Answer Macroscopic objects have wavelengths too
  small to interact with slits, BUT atomic-sized
  objects DO appear to behave like waves!

Macroscopic Object ping pong ball
Microscopic Object slow electron (1 speed of
light)
5
Electrons Wave-like Behavior

• Evidence for wave-like behavior of electrons
  includes
• Diffraction/interference patterns formed by one
  or more electrons passing through micromachined
  slits (see below).
• Diffraction patterns formed by a low energy
  electron beam impinging on periodic atomic
  lattice of a crystal surface (LEED).

Double-Slit Electron Diffraction Pattern

• Each dot indicates electron hitting a screen
  located past the slit.
• Dot locations are determined by a probabilistic
  process, where multiple electrons build up the
  diffraction pattern normally observed for light.

6
Electron Diffraction Shortcut l Calculation

• For LEED experiments, the electron wavelength l
  must be known.

• For accelerating voltage Vo 100 V, l 0.12 nm
  (atomic spacing).

7
Photons Electromagnetic Spectrum
400 nm
Gamma Rays
X-Rays
Ultraviolet
Visible Spectrum
Visible
Frequency
Wavelength
Infrared
Microwave
Short Radio Waves
TV and FM Radio
AM Radio
Long Radio Waves
700 nm
8
Blackbody Radiation Photons from hot object

• Temperature of a body is proportional to its
  average translational kinetic energy.
• Emitted Energy Thermal Radiation (red 500 oC)
• Increasing Temp Energy (or photons) absorbed via
  oscillating atoms.
• Decreasing Temp Energy emitted via oscillating
  electrons.
• Constant Temp Equal rates of energy absorption
  and emission
• Ideal Blackbody absorbs ALL incident radiation
  and re-emits it.

Ideal Blackbody
Only absorbed and emitted radiation, no reflected
radiation
9
Blackbody Radiation Stefan-Boltzmann Relation

• R Radiation intensity, T Temp. in Kelvin, s
  5.6710-8 W/m2K4
• For non-ideal black body, R sT4E where E
  emissivity lt 1.

Experimental Spectral Distribution
Long l
Short l
10
Blackbody Radiation Wiens Law
Lower Temps
Spectral Distribution depends ONLY on Temperature.
Sunlight
11
Blackbody Spectrum Rayleigh-Jeans Equation
where Eave average energy per mode kT from
Boltzmann distribution n(l) number
of oscillation modes of cavity
Rayleigh-Jeans

• Raleigh-Jeans equation behaves well at long l
  (low energy).
• BUT, explodes to infinity for short l (high
  energy).? UV catastrophe!

experiment
12
Blackbody Spectrum Plancks Law
where Eave is given by Bose-Einstein distribution
using E hc/l

• Plancks Law was initially found empirically
  (trial and error!)
• Derived from quantization of radiation, i.e.
  existence of photons!
• Limit for small l ? zero.Limit for large l ?
  Raleigh-Jeans.

Rayleigh-Jeans
Plancks Law
13
Spectral Blackbody Derivation of Eave

• OLD method uses a continuous energy distribution
  f(E) and integrates to find Eave for the
  Raleigh-Jeans equation.

• NEW method uses a discrete energy distribution
  fn(En) and uses a summation to find Eave for
  Plancks Law.

• Assumption of Energy Quantization is CRITICAL!