DIFFUSION Chapter 7

1
DIFFUSION - Chapter 7
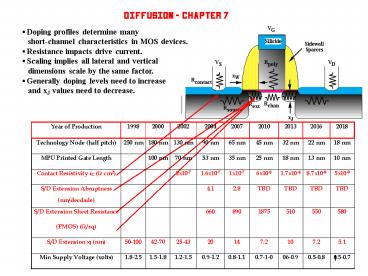
Doping profiles determine many short-channel
characteristics in MOS devices. Resistance
impacts drive current. Scaling implies all
lateral and vertical dimensions scale by the
same factor. Generally doping levels need to
increase and xJ values need to decrease.
2
Concept of Sheet Resistance of Doped Layers.
The resistivity of a cube is given by
W
t
The sheet resistance of a shallow junction
is
L
Resistivity
Sheet resistance
For a non-uniformly doped layer,
L/W squares
I12
V34
1
2
I23
V41
Numerically integrated by Irvin for simple
analytical profiles (later).
4
Raverage
3
Sheet resistance ?s?/sq. can be
experimentally measured by a four point probe
technique or van der Pauw. Doping profiles can
be measured by SIMS (chemical) or spreading R
(electrical).
?s?? but keep xj small to avoid DIBL (conflicting
requirements
In MOSFETs Rcontact Rsource Rext lt 10 Rchen
3
VSLS Shallow and Heavily Doped Junctions
50 nm
LDD cannot be used
4
Historical Development and Basic Concepts
1960

• Development (40 years) in predeposition
• Solid-phase diffusion from glass layer.
• Gas phase deposition at high temperatures (B2H6,
  PH3, AsH6) ? reproducibility good only for solid
  sol. (too high Ns)
• Replace predeposition by ion implantation good
  for bigger devices but difficult for small ones
  (TED)
• Return to diffusion for deep submicron devices

5
Diffusion Concepts

• Diffusion is the redistribution of atoms
• from regions of high concentration of
• mobile species to regions of low
• concentration. It occurs at all temperatures,
• but the diffusivity has an exponential
• dependence on T.
• Predeposition doping often proceeds by
• an initial predep step to introduce the
• required dose of dopant into the substrate.
• Drive-In a subsequent drive-in anneal
• then redistributes the dopant giving the
• required xJ and surface concentration.

6
Junction Formation Process Choice
PR
7
Dopant Solid Solubility
Metastable electrical activation (search for
metastable annealing?)

• Dopants are soluble in bulk silicon up to a
  maximum value before they precipitate into
  another phase.
• Concentrations above SS limits result in
  inactive complexes (defects,precipitates)

Practical concentrations for active P and As
Dopants may have an electrical solubility
that is different than the solid solubility
defined above. One example - As4V -
electrically inactive complex.
As complexes not active electrically
8
Diffusion from a Microscopic Viewpoint
Macroscopic dopant redistribution is described
by Ficks first law, which describes how the flux
(or flow) of dopant depends on the doping
gradient.
D is the diffusivity (cm2 sec-1). D is
isotropic in the silicon lattice. Ficks
second law describes how the change in
concentration in a volume element is
determined by the fluxes in/out of the volume.
D const.
Df(N)
If D is a constant this gives
D const
This is rarely true in practice but this is
the only form of Fick's second law which can
be solved analytically.
9
Analytic Solutions Of Ficks Laws

• Limited Source Consider a fixed dose Q,
  introduced as a delta function at the origin.

The solution that satisfies Ficks second law is
?f(t) Cabx

• In steady state ( )

?-epi layer Ion implant Very short diffusion

• For Infinite medium
• Boundary conditions

Dose
C ?with vtime
L2v(Dt)
Diffusion length

• Important consequences
• 1. Dose Q remains constant
• 2. Peak concentration decreases as time
  increases
• 3. Diffusion distance increases as time
  increases

10
Analytic Solutions Of Ficks Laws
Gaussian Solution near a Surface
2. Constant Source Near A Surface
This is similar to the previous case except
the diffusion only goes in one direction.
Assume no dopant is lost at the surface
Delta layers thickness ltlt X 2 v(Dt) (final
penetration) At the surface, if oxide growth
occurs ? dopant segregation evaporation
11
Error Function Solution in an Infinite Medium
3. Infinite Source (unlimited supply)
The infinite source is made up of small
slices each diffusing as a Gaussian.
Linear superposition ?xi
?x?0
The solution which satisfies Ficks second
law is
Deposited layer
t ?
Complementary error function
12
Error Function Solution in an Infinite Medium
Important consequences of error function
solution Symmetry about mid-point allows
solution for constant surface
concentration to be derived.
Error function solution is made up of a sum
of Gaussian delta function solutions.
Dose beyond x 0 continues to increase
with annealing time. (See Appendix A.9 in text
for properties of erfc.)
4. Constant Surface Concentration
Just the right hand side of the above figure.
Erfc function - Tabulated or approximated
Note that the dose is given by
13
Error Function Solution Near a Surface
Surface concentration set! by the solubility
limits of the dopants CS(T)
Linear scale
Log scale
Qerfc increases with time. Qgauss is constant in
time it is set by a predeposition (erfc)
preceding the diffusion (drive-in)
14
Intrinsic Dopant Diffusion Coefficients
Intrinsic dopant diffusion coefficients are
found to be of the form
(13)
EA activation energy
Note that ni is very large at process
temperatures, so "intrinsic" actually applies
under many conditions. Note the "slow"
and "fast" diffusers. Solubility is also an issue
in choosing a particular dopant.
Intrinsic Diffusion means that Ndopant lt ni _at_
diffusion T 1000 C, ni 7.14 1018cm-3 (1.45
1010 cm-3_at_ RT).
Arrhenius fit
Eg/2kT
In, B
As
P
Sb
Fast Diffusers
Slow Diffusers
15
Intrinsic Diffusion Coefficients of Dopants in
Silicon
Arrhenius fit
In, B
As
P
Sb
_at_ High dopant concentrations the diffusion will
be enhanced. That will cause profiles distortions
16
Effect Of Successive Diffusions
If a dopant is diffused at temperature T1 for
time t1 and then is diffused at temperature
T2 for time t2, the total effective Dt is given
by the sum of all the individual Dt products.
The Gaussian solution only holds if the Dt used
to introduce the dopant is small compared
with the final Dt for the drive-in i.e. if an
initial delta function approximation is
reasonable. Example In a bipolar transistor,
if the emitter profile is formed by a predep and
the base profile by an implant drive-in,
then the junctions occur where
(Emitter Dt) (BaseEmitter Dt)
17
Successive Diffusion Steps
Dt is a measure of thermal budget
_at_ one T
T1 followed by T2
Equivalent time
Transient Enhanced Diffusion (TED) and
Concentration Enhanced Diffusion (CED) when D
increases with C and/or crystallographic/point
defects
Use Computer Simulation must include diffusion
enhancement
Wolf, VLSI Era
18
Design Of Diffused Layers
The equation
has been numerically integrated for
specific cases (erfc and Gaussian). Example of
Irvins curves, in this case for P type
Gaussian profiles. (Other examples are in
Appendix A.8 in the text.)
Important Rs, Cs, xj Surface Concentration
determined from Rs (or ?s) and xj measurements
Irvins curves for erfc and Gaussian profiles
19
Design and Evaluation of Diffused Layer
We can now consider how to design a boron
diffusion process (say for the well or tub of
a CMOS process - Figs. 2.10 - 2.12), such
that

Example Design a B diffusion process
?s900?/sq., xj 3 µm for substrate CB 1015 cm-3
Pick 1100 C? D1.5 10-13 cm2sec-1 t 6.8 hour
(ex. the well process)
Use QC(0,t)(?Dt)1/24.31013 cm-2 implanted
or predeposition (initial dose)
From predeposition_at_ 950 C, Csol.sol2.51020cm-3,
D4.21015 cm2sec-1 not valid since
Cs_predepositiongtgtni
Delta function approx. Dtpredep2.310-14ltlt
Dtdrivein3.710-9
So Gaussian distribution is correct for the
drive-in process
20
(More of the step by step approach)
The average conductivity of the layer is
From Irvins curve we obtain
We can surmise that the profile is Gaussian
after drive-in.
so that
If the drive-in is done at 1100 C, then
the boron diffusivity is
The drive-in time is therefore
21
Manufacturing Methods and Equipment
Furnaces horizontal, vertical (100 C/min ramp)
Temperatures 800-1100 C, N2 (O2 low ) or Ar,
O2 when oxide must be grown
So ?? with T (but can it be ignored during
ramping?)
750-800 C_at_ 5-10C/min to 1000-1100 C
(?warpage)
For TED defects induced by implantation show ?? D
at low T compared to high T.

• RTA goalno diffusion but damage annealing/dopant
  activation
• Issues
• 100 C/sec ramp
• Single wafer processing.
• 1-100 sec process.
• Wafer T and uniformly measurement and control.

22
Measurement Methods
SIMS Secondary Ion Mass Spectroscopy
sensitivity 1016 1017 cm-3. Analysis of chemical
concentration of dopants (both active and non
active)
Mass analyzed and counted ? C(X) Test areas may
be included on an IC wafer
As, P, Sb ? bombarded with Cs as primary ions ?
produce dopant ions. Required high ion yield,
small mass interference) B, In ? O (oxygen)

• Knock on incident beam recoils atoms into the
  substrate(? with ion mass CsgtO ? degrades depth
  resolution
• Sputtering rate at the surface increased by
  oxide? use lower energies down to 200 eV- 5keV to
  decrease sputtering (important for shallow
  junctions)
• Multilayer structures show matrix effect
  (sputtering yield and ion yield) and mixing
  (heavy Cs)
• Use oxygen bleed keep ionization yield
  constant.

Problems
23
Spreading Resistance
R(x) ? ?(x) ? n(x) Compare with C(x) from SIMS to
get dopant activation. (information on defects,
clusters etc.)
8- 34
SIMS
R
From Wolf, VLSi Era
x
junction
24
Sheet resistance Four point probe. (Figure 3.12)
for shallow junctions use the Van De Pauw
structure Capacitance Voltage C-V of a MOS
Capacitor ? C ?XD(V) ? xD(N) ? N(x) TEM Cross
Section
Preparation of samples Very complex Delineation
by etching the doped silicon in HF HNO3CH3COOH
1 40 20 Doped silicon etch rate depends on
dopant concentrations
25
2D Electrical Measurements Using Scanning Probe
Microscopy
Random distribution depends on the doping
concentrations 1.3nm _at_ 1020 cm-3, 6.2 nm _at_ 1018
cm-3, 28.8 nm_at_ 1016 cm-3
STM Scanning Tunneling Microscopy not useful ?
scanning capacitance (from STM or rather AFM)
and Scanning Resistance. Problems
Cross-Sectionpreparation hard, Image
interpretation (C?N)
For soft contact
Oxide on
Scanning resistance - as in SRP but better
control of the probes (cantilever)
Inverse Electrical Measurements I-V, C-V of
devices may not match simulated characteristics ?
make corrections as to the doping profiles.