Linear Wave Theory fundamental description:

1
Overview of Waves and Sediment Transport Most
energy on continental shelf - gravity waves
consisting of sea and swell
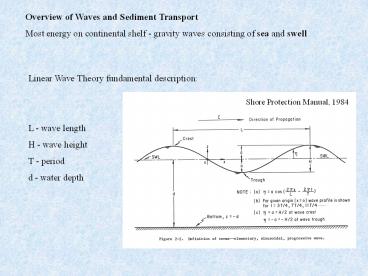
Linear Wave Theory fundamental description L -
wave length H - wave height T - period d - water
depth
Shore Protection Manual, 1984
2
(Jeff Parsons web site)
3
Wave theory characteristics that affect what we
see in the bottom boundary layer When wave is in
deep water - d/L gt 1/2 orbits circular waves
dont feel the bottom (and the seabed doesnt
feel the waves) When wave is in shallow water
- d/L lt 1/25 orbits flatten, become
elliptical wave speed is dependent upon depth, c
(gd)1/2 wave-orbital velocities are felt at the
seabed
4
Linear Wave Theory
Shore Protection Manual, 1984
5
Key Linear Wave equations for sediment
transport (At bottom, z -d ) Wavelength Maxi
mum wave-orbital velocity, cos(T) 1 Orbital
Excursion
6
Example On the Washington shelf, a winter storm
could produce waves of 7 m in height with period
of 15 seconds. At what depths are these waves
felt on the shelf?
7
Shallow water waves Speed is dependent on water
depth wave speed, c(gd)1/2
Leads to wave refraction as shoreline is
approached.
8
Wave boundary layer Linear wave theory assumed
inviscid flow (no friction at bed). We can use
linear wave theory above the BBL and develop a
viscous boundary layer at seabed. Because waves
oscillate, there is limited time for viscous
effects to build. Therefore, the wave boundary
layer is thin relative to the current boundary
layer. Results in high shear in u high uw high
?b Wave boundary layer thickness is seldom gt 10
cm
9
How do we determine shear stress due to waves? 1.
Eddy viscosity concept Az ? uw z (time
invariant) 2. Wave friction factor (analogous to
a drag coefficient) Time averaged over a wave
cycle
10
What is fw a function of bed roughness,
ks orbital excursion, ab R
In rough turbulent region,
11
Alternatively, we can write the Shields
entrainment function using fw Plot with the
uni-directional threshold curve
12
Suspended sediment concentration profile under
waves (combined waves and currents) Rouse
Equation
for z lt ?cw for z gt ?cw