The Interaction of Light and Matter: a and n

1
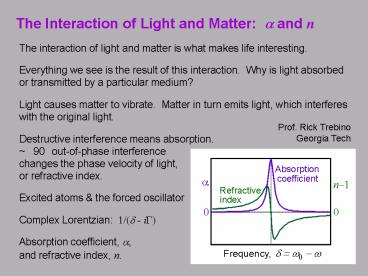
The Interaction of Light and Matter a and n

• The interaction of light and matter is what makes
  life interesting.
• Everything we see is the result of this
  interaction. Why is light absorbed or
  transmitted by a particular medium?
• Light causes matter to vibrate. Matter in turn
  emits light, which interferes with the original
  light.
• Destructive interference means absorption.
  90 out-of-phase interference changes the phase
  velocity of light, or refractive index.
• Excited atoms the forced oscillator
• Complex Lorentzian 1/(d - iG)
• Absorption coefficient, a, and refractive index,
  n.

Prof. Rick Trebino Georgia Tech
Absorption
coefficient
a
n1
Refractive
index
0
0
d w0 - w
Frequency,
2
Adding complex amplitudes

• When two waves add together with the same complex
  exponentials,
• we add the complex amplitudes, E0 E0'.

Destructive interference
Constructive interference
"Quadrature phase" 90 interference
1.0 -0.2 0.8
1.0 0.2 1.2
1.0 -0.2i 1-0.2i






Slower phase velocity
Laser
Absorption
3
Light excites atoms, which emit light that adds
(or subtracts) with the input light.

• When light of frequency w excites an atom with
  resonant frequency w0

Electric field at atom
Electron cloud
Emitted field
On resonance (w w0)
An excited atom vibrates at the frequency of the
light that excited it and re-emits the energy as
light of that frequency. The crucial issue is
the relative phase of the incident light and this
re-emitted light. For example, if these two
waves are 180 out of phase, the beam will be
attenuated. We call this absorption.
4
What do you think is happening here?
5
The Forced Oscillator
When we apply a periodic force to a natural
oscillator (such as a pendulum, spring, swing, or
atom), the result is a forced oscillator.
Examples Child on a swing being pushed
Pushed pendulum Bridge in wind or an
earthquake Electron in a light wave
Nucleus in a light wave
Tacoma Narrows Bridge collapsing because
oscillatory winds blew at its resonance frequency.
The forced oscillator is one of the most
important problems in physics. It is the concept
of resonance.
6
The Forced Oscillator The relative phaseof
the oscillator motion with respect to the
input force depends on the frequencies.
Force
Oscillator

• Below resonance
• w ltlt w0

Weak vibration.In phase.
Strong vibration.90 out of phase.
On resonance w w0
Let the oscillators resonant frequency be w0,
and the forcing frequency be w. We could think of
the forcing function as a light electric field
and the oscillator as a nucleus of an atom in a
molecule.
Weak vibration.180 out of phase.
Above resonance w gtgt w0
7
The relative phase of an electron clouds motion
with respect to input light depends on the
frequency.
Electric field at atom
Electron cloud
Below resonance w ltlt w0
Weak vibration.180 out of phase.
On resonance w w0
Strong vibration.-90 out of phase.
Let the atoms resonant frequency be w0, and the
light frequency be w.The electron charge is
negative, so theres a 180 phase shift in all
cases (compared to the previous slides plots).
Above resonance w gtgt w0
Weak vibration.In phase.
8
The relative phase of emitted light with respect
to the input light depends on the frequency.
Electric field at atom
Electron cloud
Emitted field
Below resonance w ltlt w0
Weak emission.90 out of phase.
Strong emission.180 out of phase.
On resonance w w0
The emitted light is 90 phase-shifted with
respect to the atoms motion.
Weak emission.-90 out of phase.
Above resonance w gtgt w0
9
The Forced Oscillator Math

• Consider an electron on a spring with position
  xe(t), and driven by
• a light wave, E0 exp(-iw t)

The solution is
So the electron oscillates at the incident light
wave frequency (w), but with an amplitude that
depends on the difference between the frequencies.
10
Checking our solution
Substitute the solution for xe(t) into the forced
oscillator equation to see if it works.
QED
11
The problem with this model
Exactly on resonance, when w w0, xe goes to
infinity. This is unrealistic. Well need to
fix this.
12
The Damped Forced Oscillator

• Our solution has infinite amplitude on resonance,
  which is unrealistic. We fix this by using a
  damped forced oscillator a harmonic oscillator
  experiencing a sinusoidal force and viscous drag.
  

We must add a viscous drag term
The solution is now
The electron still oscillates at the light
frequency and with a potential phase shift, but
now with a finite amplitude for all w.
13
Why we included the damping factor, g
Atoms spontaneously decay to the ground state
after a time. Also, the vibration of a medium is
the sum of the vibrations of all the atoms in the
medium, and collisions cause the sum to cancel.
Collisions dephase the vibrations,
causing cancellation of the total medium
vibration, typically exponentially. (We can use
the same argument for the emitted light, too.)
14
The atoms response is approximately a Complex
Lorentzian.

• Consider

Assuming , this becomes
In terms of the variables d w0 - w and G
g /2, the function 1/(d iG ), is called a
Complex Lorentzian. Its real and imaginary parts
are
15
Complex Lorentzian
16
Damped forced oscillator solution for
light-driven atoms

• The forced-oscillator response is sinusoidal,
  with a frequency-
• dependent strength that's approximately a complex
  Lorentzian

Here, e lt 0.
When w ltlt w0, the electron vibrates 180 out of
phase with the light wave When w w0, the
electron vibrates -90 out of phase with the
light wave When w gtgt w0, the electron vibrates
in phase with the light wave
17
The relative phase of an electron clouds motion
with respect to input light depends on the
frequency.
Electric field at atom
Electron cloud
Weak vibration.180 out of phase.
Below resonance w ltlt w0
On resonance w w0
Strong vibration.-90 out of phase.
Recall that the atoms resonant frequency is w0,
and the light frequency is w.
Weak vibration.In phase.
Above resonance w gtgt w0
18
Okay, so weve determined what the light wave
does to the atom.
Now, what does the atom do to the light wave?
19
Re-emitted light from an excited atominterferes
with original light beam

• The re-emitted light may interfere
  constructively, destructively, or, more
  generally, somewhat out of phase with the
  original light wave.
• We model this process by considering the total
  electric field,

E(z,t) Eoriginal(z,t) Ere-emitted(z,t)
Maxwell's Equations will allow us to solve for
the total field, E(z,t). The input field will be
the initial condition.
20
The Inhomogeneous Wave Equation

• The induced polarization, , is due to the
  medium

x
where
and e is the electron charge, and N the
electron number density.
For our vibrating electrons
E(z,t)
21
The electric-field amplitude depends on z.

• The effect of the medium will be to change the
  field complex amplitude with distance. And
  because the polarization depends on E, its
  amplitude, P0, will also.

Constant in time
Specifically, the envelopes, E0(z) and P0(z), are
assumed to vary slowly the fast variations will
all be in the complex exponential. The time
derivatives are easy (as before, they just
multiply by a factor of w2) because the
envelopes are independent of t
22
The Slowly Varying Envelope Approximation

• But the ?2E/ ?z2 derivative is trickier.

The z-derivatives
Because variations of the envelope, E0(z), in
space will be slow, well neglect the 2nd
z-derivative.
23
SVEA continued

• Substituting the derivatives into the
  inhomogeneous wave equation

Now, use k w/c. And canceling the complex
exponentials leaves
24
Why the re-emitted light is 90 out of phase with
the polarization
Usually, P0 P0 (E0), and hence P0(z), too. But
consider for the moment P0 constant.
Converting to finite differences, the re-emitted
field is just DE0, and it will be
Note the i, which means that the re-emitted field
has a 90 phase shift with respect to the
polarization and hence a -90 phase shift with
respect to the electron cloud motion.
25
The re-emitted wave leads the electron cloud
motion by 90 in phase.
Electric field at atom
Electron cloud
Emitted field
Below resonance w ltlt w0
Weak emission.90 out of phase.
On resonance w w0
Strong emission.180 out of phase.
This phase shift adds to the potential phase
shift of the electron cloud motion with respect
to the input light.
Weak emission.-90 out of phase.
Above resonance w gtgt w0
26
Solving for the slowly varying envelope
Define c, the susceptibility

• Substituting for P0 ,
  becomes

The solution
Define new quantities for the real and imaginary
parts of c
so that
where a is the absorption coefficient and n is
the refractive index.
27
The complete electric field in a medium

• The electromagnetic wave in the medium becomes
  (combining the
• slowly varying envelope with the complex
  exponential)
• Simplifying

E0(z)
Absorption
Refractive index attenuates the field
changes the k-vector
To summarize, in a medium
28
A light wave in a medium
Vacuum (or air)
Medium
n 1
n 2
l0
Absorption depth 1/a
k0
nk0
Wavelength decreases
l0/n
The speed of light, the wavelength (and k), and
the amplitude change, but the frequency, w,
doesnt change.
29
Absorption Coefficient and the Irradiance

• The irradiance is proportional to the (average)
  square of the field.
• Since E(z) µ exp(-az/2), the irradiance is then

I(z) I(0) exp(-a z)
where I(0) is the irradiance at z 0, and I(z)
is the irradiance at z. Thus, due to absorption,
a beams irradiance exponentially decreases as it
propagates through a medium. The 1/e distance,
1/a, is a rough measure of the distance light can
propagate into a medium (the penetration depth).
30
Refractive index and Absorption coefficient

• n comes from the real part of c

a comes from the imaginary part of c
Simplifying
These results are valid for small values of these
quantities.
31
Refractive index and Absorption coefficient
w0
Frequency, w
32
Different atoms have different resonancefrequenci
es, w0, and widths, g.

•  

33
Molecules have a higher density of states than
atoms and so have much more complex absorption
spectra.
Due to the finite width of absorptions, these
levels can overlap.
2nd excited electronic state
Actually, its not correct to broaden a single
level its really each pair of levels that
broadens.
Energy
1st excited electronic state
In any case, a batch of identical molecules can
be highly absorbing over a large spectral range.
Ground electronic state
34
The absorption of glass
Transmission ranges for various glasses
Its difficult to find transparent materials
below 100 nm and above 70 mm.
35
Absorbing glass filters
A wide range of absorbing glass filters allow us
to manipulate the spectrum of a light beam. A red
filter transmits red light, etc.
36
What determines the color of an object?
The wavelengths that are not absorbed will be
reflected and/or scattered into our eyes.
These filters transmit only one color region
(red, green or blue)
These filters transmit only two color regions (a
yellow filter transmits red and green)
37
RGB vs. CMYK
Additive color (RGB) is used for light emanating
directly from a light source. Red and green light
add to yield yellow. Subtractive color (CMYK) is
used for inks and dyes that reflect light from an
object. Inks and dyes absorb light and so
subtract light from the white light incident on a
surface.
RGB is used for TVs and monitors. CMYK is used
for printing.
38
Why are most plants green and then red or yellow
in the fall?
Chlorophyll absorbs in the red and blue, and
hence reflects in the green. But it breaks down
in the fall.
In the fall, trees produce carotenoids, which
reflect yellow, and anthocyanins, which reflect
orange and red. Biologists believe that these
molecules ward off insects.
39
Materials that are transparent in the IR can be
opaque in the visible.
And materials that are opaque in the visible are
often transparent in the IR. (You can try this
at home with your IR remote control!)
40
By choosing a high-power laser that is absorbed
by a material, we can laser-weld or cut.
Here, a CO2 laser, which lases at 10.6 mm, cuts
metal. Laser surgery works on the same principle.
41
The suns emission spectrum in the visible
The dark lines below represent absorption due to
elements on the surface of the sun from its
various constituents.
42
Actual sunlight spectrum reaching earths surface
43
Absorption spectrum of air
Air consists of numerous molecules that are
non-absorbing in the visible, but which can
absorb very strongly elsewhere.
I(z) I(0) exp(-a z) Attenuation
I(z)/I(0) exp(-a z)
-log(Attenuation) a z
Note the large variation in attenuation, i.e.,
absorption!
44
Waters absorption distance vs. wavelength
Penetration depth into water vs. wavelength
1 km
Water is clear in the visible, but not elsewhere.
UV
IR
X-ray
Microwave
1 m
Radio
Penetration depth into water (1/a)
1 mm
Notice that the penetration depth varies by over
ten orders of magnitude!
1 µm
1 km
1 m
1 mm
1 µm
1 nm
Wavelength
Visible spectrum
45
Measuring Lake Purity
46
Illuminating a water droplet with different
wavelengths
Water droplet
Light passes through droplet no energy is
absorbed. Nothing happens to droplet.
Visible light
Light is absorbed in several microns. Water is
vaporized, yielding massive droplet acceleration
in the forward direction.
Excited region
2.78-µm light (ErCrYSGG)
Laser-accelerated water droplets are now being
used by dentists to cut teeth!
47
Absorption Spectrum of Human Tissue
48
Absorption in optical fibers
This is why optical telecommunications occur at
1550 nm.
49
Dispersion is the tendency of optical properties
to depend on frequency.
Dispersion of the refractive index allows prisms
to separate white light into its components and
to measure the wavelength of light.
n(l)
Dispersion can be good or bad, depending on what
youd like to do.
50
Refractive Index vs. Wavelength

• Since resonance frequencies exist in many
  spectral ranges, the refractive index varies in a
  complex manner.

Electronic resonances usually occur in the UV
vibrational and rotational resonances occur in
the IR and inner-shell electronic resonances
occur in the x-ray region. n increases with
frequency, except in anomalous dispersion regions.
51
Refractive indices for glasses in the UV,
visible, and IR
Well use n 1.5 for the refractive index of
the glass we usually encounter.
52
The Sellmeier Equation approximates the
refractive-index curve for most materials.
These values are obtained by measuring n for
numerous wavelengths and then curve-fitting.
53
Practical numbers for material dispersion
dn/dl (1/mm)
54
Refractive Index and the Speed of Light

• The speed of light is w/k. Since k0 becomes k
  nk0 in a medium,
• where c0 is the speed of light in vacuum.
• The refractive index, n, of a medium is thus the
  ratio of the speed
• of light in vacuum to the speed of light in the
  medium. It can be
• defined as the ratio
• The refractive index is usually gt 1. But it can
  be lt 1.

55
The Irradiance in a medium

• The irradiance
•  
•  
• Substitute for c in the medium c c0 /n
•  
• Now we need e n c0 /c, but c0 1/ve0m0 and
  c 1/vem and m m0
• so n ve /ve0
• e e0 n2
•  
•  
• So the irradiance in the medium becomes
  
• or
•  
•  

56
Refraction and Snell's Law
The electric field (and its wave-fronts) are
continuous at a boundary. But the speed of light
will be different in the two media.

• AD BD/sin(qi)
• AD AE/sin(qt)
• So BD/sin(qi) AE/sin(qt)
• But BD vi Dt (c0 /ni) Dt
• AE vt Dt (c0 /nt ) Dt
• So (c0 /ni) Dt / sin(qi)
• (c0 /nt) Dt / sin(qt)
• Or ni sin(qi) nt sin(qt)

ni
nt
57
Snell's Law for many parallel layers
If the layers are parallel, then these angles are
always equal.

• So we can ignore the intermediate layers if were
  only interested in the output angle!

58
Snells Law causes things to look bent in water.
59
Snell's Law explains many everyday effects

• The refractive index increases with density (and
  hence decreases with temperature at a given
  altitude).

Occasionally, astronomers speculate whether light
can orbit a planet somewhere in the
universe This effect may play a role in mirages.
60
Snells Law explains why the sun flattens as it
sets.
Light rays closer to the horizon bend more than
rays further away.
61
The Green Flash
Just as the sun sets, there is a green flash for
a fraction of a second.
Its due to the same refractive ray curvature
that flattens the sun, but the long path that
light takes through the atmosphere at sunset
allows an otherwise unseen atmospheric absorption
in the yellow to split the suns spectrum into
orange and green components.
62
Snells Law explains why stars twinkle.
The atmosphere has non-uniform temperature and
hence non-uniform refractive index. And these
regions move about in time.
Star
Cooler regions of air (with higher refractive
index)
As the air masses move about, the amount of light
reaching our eyes from the star varies.
63
Refraction allows prisms to expand or compress a
beam.
Magnification (or demagnification) occurs at both
surfaces.
din
dout
64
Refraction causes prisms to disperse light.

• Because the refractive index depends on
  wavelength, the refraction angle also depends on
  wavelength this is called angular dispersion.

Because n generally decreases with wave- length
(dn/dl lt 0), the shorter the wavelength, the
greater the refraction angle.
Input white beam
n(l)
Dispersed beam
Prism
Suppose light enters the prism at 0, and qtint
is its incidence angle at the exit face.
Differentiating implicitly w.r.t. l We obtain
the prism dispersion
65
More generally, prisms disperse light at both
surfaces.
The dispersion of a general prism is
Dispersion at exit face, dt
Magnification at exit face, mt
Dispersion at entrance face, di
66
The dispersion of a series of prisms
Let Di be the dispersion of the ith prism (Di is
positive for upward-pointing prisms and negative
for downward-pointing prisms) and Mi be the
magnification of the ith prism. The total
dispersion of all the prisms will be
The contribution of each prisms dispersion is
reduced by the total magnification after it!
67
Refraction makes lenses possible.
Because refraction bends rays toward the thickest
part of a lens, parallel rays incident on a
convex lens converge.
The distance at which parallel rays converge is
the lens focal length, f.
68
Dispersion is undesirable in lenses.
Unfortunately, dispersion also causes lenses to
focus different colors at different distances,
making lens design difficult. This is called
chromatic aberration.
Lens designers go to great lengths to compensate
for dispersion.
69
Angle of Incidence Angle of Reflection
The electric field wave-fronts are continuous at
a boundary. The speed of light is the same in
the incident and reflected media (because theyre
the same). Let qr be the reflected-beam
propagation angle.
ni

• AD BD/sin(qi) AD AE/sin(qr)
  BD/sin(qi) AE/sin(qr)
• But BD vi Dt (c0 /ni) Dt
  AE vt Dt (c0 /ni) Dt
• So (c0 /ni) Dt / sin(qi)
  (c0 /ni) Dt / sin(qr)
• Or sin(qi) sin(qr)
  qi qr

70
Rainbows result from dispersion in the refraction
of sunlight in water droplets.

• Note that there can be two rainbows, and the top
  one is inverted.

And the sky is much brighter below the bottom one.
71
Rainbow explanation Light in a spherical droplet
Light paths
Water droplet

• Light can enter a droplet at different distances
  from its edge.

We must compute the angle of the emerging light
as a function of the incident position.
For a cool java applet showing this, try
http//users.erols.com/renau/rainbow.html
72
Plotting deflection angle vs. wavelength is the
key.
Because n varies with wavelength, the minimum
deflection angle varies with color.
Lots of violet deflected at this angle
Lots of red deflected at this angle
Lots of light of all colors is deflected by
gt138, so the region below rainbow is bright and
white.
73
Explanation of 2nd rainbow

• The 2nd (upper) rainbow results from light
  entering the droplet
• in its lower half and making 2 internal
  reflections in the droplet.

Water droplet
Minimum deflection angle (232.5) yielding a
rainbow radius of 52.5.
Because energy is lost at each reflection, the
2nd rainbow is weaker. 3rd and 4th rainbows are
weaker, more spread out, and toward the sun. 5th
rainbow overlaps 2nd, and 6th is below the 1st,
but too weak to see.