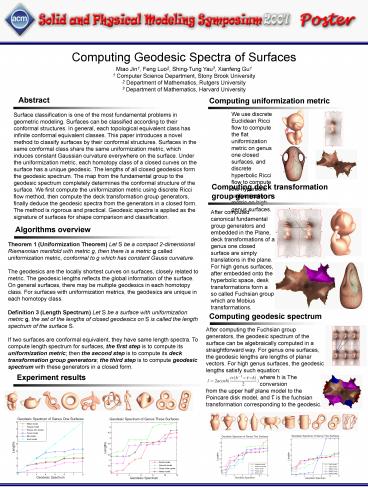
Computing Geodesic Spectra of Surfaces

1
Computing Geodesic Spectra of Surfaces
Miao Jin1, Feng Luo2, Shing-Tung Yau3, Xianfeng
Gu1 1 Computer Science Department, Stony Brook
University 2 Department of Mathematics, Rutgers
University 3 Department of Mathematics, Harvard
University
Abstract
Computing uniformization metric
We use discrete Euclidean Ricci flow to compute
the flat uniformization metric on genus one
closed surfaces, and discrete hyperbolic Ricci
flow to compute the hyperbolic uniformization
metric on high genus surfaces.
Surface classification is one of the most
fundamental problems in geometric modeling.
Surfaces can be classified according to their
conformal structures. In general, each
topological equivalent class has infinite
conformal equivalent classes. This paper
introduces a novel method to classify surfaces by
their conformal structures. Surfaces in the same
conformal class share the same uniformization
metric, which induces constant Gaussian curvature
everywhere on the surface. Under the
uniformization metric, each homotopy class of a
closed curves on the surface has a unique
geodesic. The lengths of all closed geodesics
form the geodesic spectrum. The map from the
fundamental group to the geodesic spectrum
completely determines the conformal structure of
the surface. We first compute the uniformization
metric using discrete Ricci flow method, then
compute the deck transformation group generators,
finally deduce the geodesic spectra from the
generators in a closed form. The method is
rigorous and practical. Geodesic spectra is
applied as the signature of surfaces for shape
comparison and classification.
Computing deck transformation group generators
After computed canonical fundamental group
generators and embedded in the Plane, deck
transformations of a genus one closed surface are
simply translations in the plane. For high genus
surfaces, after embedded onto the hyperbolic
space, desk transformations form a so called
Fuchsian group which are Mobius transformations.
Algorithms overview
Theorem 1 (Uniformization Theorem) Let S be a
compact 2-dimensional Riemannian manifold with
metric g, then there is a metric g called
uniformization metric, conformal to g which has
constant Gauss curvature. The geodesics are the
locally shortest curves on surfaces, closely
related to metric. The geodesic lengths reflects
the global information of the surface. On general
surfaces, there may be multiple geodesics in each
homotopy class. For surfaces with uniformization
metrics, the geodesics are unique in each
homotopy class. Definition 3 (Length Spectrum)
Let S be a surface with uniformization metric g,
the set of the lengths of closed geodesics on S
is called the length spectrum of the surface
S. If two surfaces are conformal equivalent,
they have same length spectra. To compute length
spectrum for surfaces, the first step is to
compute its uniformization metric then the
second step is to compute its deck transformation
group generators the third step is to compute
geodesic spectrum with these generators in a
closed form.
Computing geodesic spectrum
After computing the Fuchsian group generators,
the geodesic spectrum of the surface can be
algebraically computed in a straightforward way.
For genus one surfaces, the geodesic lengths are
lengths of planar vectors. For high genus
surfaces, the geodesic lengths satisfy such
equation where h is The
conversion from the upper half plane model to the
Poincare disk model, and is the fuchsian
transformation corresponding to the geodesic.
Experiment results