Chapter 1 Chemistry and Measurement

1
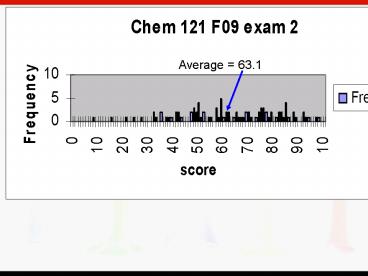
Average 63.1
2
Average138C
A 185 B-140-150 A- 176-184
C125-139 B166-175 C 110-124 B151-165
C- 94-109
3
Chapter 7Quantum Theory of the Atom
4

• Einstein used this understanding of light to
  explain the photoelectric effect in 1905.
• Each electron is struck by a single photon. Only
  when that photon has enough energy will the
  electron be ejected from the atom that photon is
  said to be absorbed.

5

• Light, therefore, has properties of both waves
  and matter. Neither understanding is sufficient
  alone. This is called the particlewave duality
  of light.

6

• The bluegreen line of the hydrogen atom spectrum
  has a wavelength of 486 nm. What is the energy of
  a photon of this light?

E hn and c nl so E hc/l
l 4.86 nm 4.86 10-7 m c 3.00 108 m/s h
6.63 10-34 J ? s
l 4.09 10-19 J
7

• In the early 1900s, the atom was understood to
  consist of a positive nucleus around which
  electrons move (Rutherfords model).
• This explanation left a theoretical dilemma
  According to the physics of the time, an
  electrically charged particle circling a center
  would continually lose energy as electromagnetic
  radiation. But this is not the caseatoms are
  stable.

8

• In addition, this understanding could not explain
  the observation of line spectra of atoms.
• A continuous spectrum contains all wavelengths of
  light.
• A line spectrum shows only certain colors or
  specific wavelengths of light. When atoms are
  heated, they emit light. This process produces a
  line spectrum that is specific to that atom. The
  emission spectra of six elements are shown on the
  next slide.

9
Light and Atoms

• When an atom gains a photon, it enters an excited
  state.
• This state has too much energy - the atom must
  lose it and return back down to its ground state,
  the most stable state for the atom.
• Line spectra indicate light emitted when excited
  electrons lose energy.
• An energy level diagram is used to represent
  these changes.

10
(No Transcript)
11

• In 1913, Neils Bohr, a Danish scientist, set down
  postulates to account for
• 1. The stability of the hydrogen atom
• 2. The line spectrum of the atom

12

• Energy-Level Postulate
• An electron can have only certain energy values,
  called energy levels. Energy levels are
  quantized.
• For an electron in a hydrogen atom, the energy is
  given by the following equation
• RH 2.179 x 10-18 J
• n principal quantum number

13

• Transitions Between Energy Levels
• An electron can change energy levels by absorbing
  energy to move to a higher energy level or by
  emitting energy to move to a lower energy level.

14
Energy Level Diagram

• Energy
• Excited States
• photons path
• Ground State

Light Emission Light Emission
Light Emission
15

• For a hydrogen electron the energy change is
  given by

RH 2.179 10-18 J, Rydberg constant
16

• The energy of the emitted or absorbed photon is
  related to DE
• We can now combine these two equations

17

• Light is absorbed by an atom when the electron
  transition is from lower n to higher n (nf gt ni).
  In this case, DE will be positive.
• Light is emitted from an atom when the electron
  transition is from higher n to lower n (nf lt ni).
  In this case, DE will be negative.
• An electron is ejected when nf 8.

18

• Energy-level diagram for the hydrogen atom.

19

• Electron transitions for an electron in the
  hydrogen atom.

20

• What is the wavelength of the light emitted when
  the electron in a hydrogen atom undergoes a
  transition from n 6 to n 3?

ni 6 nf 3 RH 2.179 10-18 J
-1.816 x 10-19 J
1.094 10-6 m
21
(No Transcript)
22
A minimum of three energy levels are required.

• The red line corresponds to the smaller energy
  difference in going from n 3 to n 2. The blue
  line corresponds to the larger energy difference
  in going from n 2 to n 1.

23
Planck Vibrating atoms have only certain
energies E hn or 2hn or 3hn Einstein Energy is
quantized in particles called photons E
hn Bohr Electrons in atoms can have only certain
values of energy. For hydrogen
24

• Light has properties of both waves and particles
  (matter).
• What about matter?

25

• In 1923, Louis de Broglie, a French physicist,
  reasoned that particles (matter) might also have
  wave properties.
• The wavelength of a particle of mass, m (kg), and
  velocity, v (m/s), is given by the de Broglie
  relation

26

• Compare the wavelengths of (a) an electron
  traveling at a speed that is one-hundredth the
  speed of light and (b) a baseball of mass 0.145
  kg having a speed of 26.8 m/s (60 mph).

Electron me 9.11 10-31 kg v 3.00 106 m/s
Baseball m 0.145 kg v 26.8 m/s
27
Electron me 9.11 10-31 kg v 3.00 106 m/s
2.43 10-10 m
Baseball m 0.145 kg v 26.8 m/s
1.71 10-34 m
28
(No Transcript)
29
(No Transcript)
30

• Building on de Broglies work, in 1926, Erwin
  Schrödinger devised a theory that could be used
  to explain the wave properties of electrons in
  atoms and molecules.
• The branch of physics that mathematically
  describes the wave properties of submicroscopic
  particles is called quantum mechanics or wave
  mechanics.

31

• Quantum mechanics alters how we think about the
  motion of particles.
• In 1927, Werner Heisenberg showed how it is
  impossible to know with absolute precision both
  the position, x, and the momentum, p, of a
  particle such as electron.
• Because p mv this uncertainty becomes more
  significant as the mass of the particle becomes
  smaller.

32

• Quantum mechanics allows us to make statistical
  statements about the regions in which we are most
  likely to find the electron.
• Solving Schrödingers equation gives us a wave
  function, represented by the Greek letter psi, y,
  which gives information about a particle in a
  given energy level.
• Psi-squared, y 2, gives us the probability of
  finding the particle within a region of space.

33

• The wave function for the lowest level of the
  hydrogen atom is shown to the left.
• Note that its value is greatest nearest the
  nucleus, but rapidly decreases thereafter. Note
  also that it never goes to zero, only to a very
  small value.

34

• Two additional views are shown on the next slide.
• Figure A illustrates the probability density for
  an electron in hydrogen. The concentric circles
  represent successive shells.
• Figure B shows the probability of finding the
  electron at various distances from the nucleus.
  The highest probability (most likely) distance is
  at 50 pm.

35
(No Transcript)
36

• According to quantum mechanics, each electron is
  described by four quantum numbers
• 1. Principal quantum number (n)
• 2. Angular momentum quantum number (l)
• 3. Magnetic quantum number (ml)
• 4. Spin quantum number (ms)
• The first three define the wave function for a
  particular electron. The fourth quantum number
  refers to the magnetic property of electrons.

37

• A wave function for an electron in an atom is
  called an atomic orbital (described by three
  quantum numbersn, l, ml). It describes a region
  of space with a definite shape where there is a
  high probability of finding the electron.
• We will study the quantum numbers first, and then
  look at atomic orbitals.

38

• Principal Quantum Number, n
• This quantum number is the one on which the
  energy of an electron in an atom primarily
  depends. The smaller the value of n, the lower
  the energy and the smaller the orbital.
• The principal quantum number can have any
  positive value 1, 2, 3, . . .
• Orbitals with the same value for n are said to be
  in the same shell.