O

1
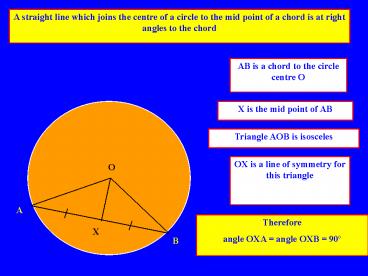
A straight line which joins the centre of a
circle to the mid point of a chord is at right
angles to the chord
AB is a chord to the circle centre O
X is the mid point of AB
Triangle AOB is isosceles
OX is a line of symmetry for this triangle
O
A
Therefore angle OXA angle OXB 90º
X
B
2
Angles in the alternate segments are equal
BX is a chord of the circle centre O
A
TX is a tangent meeting the circle at X
AX is a diameter
B
O
Prove angle BXT angle BAX
T
X
3
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
B
O
Angle ABX is 90º
angle in a semi circle
T
X
4
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
B
O
Angle OXT is 90º
angle between diameter and tangent
T
X
5
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
therefore angle AXB 90º - angle BXT
B
O
90º-BXT
T
X
6
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
but angle AXB angle BAX angle ABX 180º
B
O
angles in a triangle
90º-BXT
T
X
7
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
since angle ABX 90º angle AXB angle BAX 90º
B
O
90º-BXT
T
X
8
Angles in the alternate segments are equal
Prove angle BXT angle BAX
A
since angle ABX 90º angle AXB angle BAX 90º
therefore 90º - angle BXT angle BAX 90º
B
O
90º-BXT
therefore angle BXT angle BAX
T
X