Potential Energy Surface

1
Potential Energy Surface
2
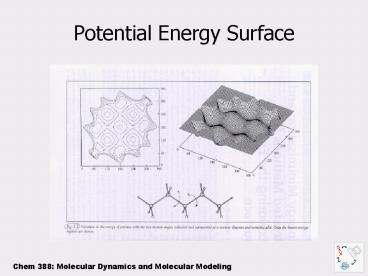
Potential Energy Surface


Local minima
Global minima

• At a maximum or minimum i.e., the gradient is
  zero, hence these are called stationary points.
• At a maximum the curvature is negative, i.e., lt
  0 (2nd derivative less than zero)
• At a minimum the curvature is positive, i.e., gt
  0 (2nd derivative more than zero)

3
For a multivariate system
curvature is determined from the 2nd partial
derivative matrix - the Hessian matrix
the gradient is the first derivative vector
4
Newton-Raphson Method
Expensive but rapidly converging
At the minimum xx, E'(x)0
5
Minimization Steepest Descent
6
Conjugate Gradient
7
Rules for Selecting Minimizer
8
Energy Surface Temp Dependence
9
20 residues 2x105 conformations 20 runs _at_ 330K
Cavali et al. (2002) Proteins 47, 6177.
10
GroEL-GroES Complex
Braig et al. (1994) Nature 371, 578. Ma et al.
(2000) JBM 302, 303. Xu et al. (1997) Nature 388,
741.
11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
(No Transcript)