Encoding

1
Encoding
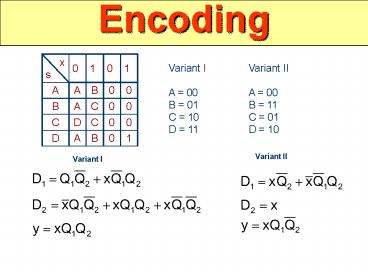
x s 0 1 0 1
A A B 0 0
B A C 0 0
C D C 0 0
D A B 0 1
Variant I A 00 B 01 C 10 D 11
Variant II A 00 B 11 C 01 D 10
Variant II
Variant I
2
Encodings
How to encode?
Can we check all possible encodings?
5 states -
140 encodings
7 states -
840 encodings
9 states -
More than 10 million encodings
3
Partition reminder
Product of partitions ?a ?b is the largest
(with respect to relation ?) partition, that is
not larger than ?a and ?b.
?b
?a
?a ?b
4
Sum of partitions
Sum of partitions ?a ?b is the smallest (with
respect to relation ?) partition, which is not
smaller than ?a and ?b.
5
Substitution Property of a partition
Partition ? on set of states of machine MltS, V,
dgt has the substitution property (closed
partition), when
Partition has the substitution property when
elements of a block under any input symbol
transit to themselves or to other block of
partition ?
6
Theorem
Given is automaton M with set of states S, S
n. To encode states we need Q1, ..., Qk memory
elements (flip-flops). If partition ? exist
with substitution property and if r among k
encoding variables Q1, ..., Qk, wherer
?log2?(,?)?, is subordinated to blocks of
partition ? such that all states included in one
block are denoted with the same variables Q1,
..., Qr , then functions Q1, ..., Qr, are
independent on remaining (k r) variables.
Conversely, if first r variables of the next
state Q1, ..., Qr (1 ? r lt k) can be
determined from the values of inputs and first r
variables Q1, ..., Qr independently on values of
the remaining variables, then there exists
partition ? with substitution property such that
two states si, sj are in the same block of
partition if and only if they are denoted by the
same value of the first r variables.
7
Serial Decomposition
Given is automaton M with set of states S.
Sufficient and necessary condition of serial
decomposition of M into two serially connected
automata M1, M2 is existence of partition ? with
substitution property and partition ? such ? ?
? 0.
8
Parallel Decomposition
Automaton M jest decomposable into two
sub-automata M1, M2 working in parallel iff in
the set of states S of this automaton there exist
two non-trivial partitions ?1, ?2 with
substitution property such that ?1 ? ?2 ?(0)
9
Serial Decomposition - Example
s12
x s 0 1 0 1
A A F 0 0
B E C 0 1
C C E 0 1
D F A 1 0
E B F 1 1
F D E 0 0
s11
s21
s22
s23
? ? ? ?(0)
State of the predecessor machine
State of primary input x
10
Serial Decomposition Example continued
x s 0 1 0 1
A A F 0 0
B E C 0 1
C C E 0 1
D F A 1 0
E B F 1 1
F D E 0 0
s12
s11
s21
s22
s23
S11ABE
S12 CDF
S21AD
M1
BC
EF
11
Parallel Decomposition-Example
s11
s12
x s 0 1 0 1
A A F 0 0
B E C 0 1
C C E 0 1
D F A 1 0
E B F 1 1
F D E 0 0
s21
s22
s23
Knowing both partitions we can create table 2,
next combining columns with the same input X we
obtain the table of one of machines
?1 ? ?2 ?(0)
ABE CDF ABE CDF
AC
BD
M2
Combining columns
EF
12
Decomposition Schemata
Serial Decomposition
Parallel Decomposition
13
Calculating a closed partition
x s 0 1
A A F
B E C
C C E
D F A
E B F
F D E
We create a graph of pairs of successors for
various initial nodes.
E
F
A,B
A,C
A,D
14
Dekompozycja z autonomicznym zegarem
Some automata have a decomposition in which we
use the autonomous clock - and sub-automaton
that is not dependent on inputs. Partition ?i of
set of states S of automaton M is compatible with
input, if for each state Sj ? S and for all vl ?
V ?(Sj,v1), ?(Sj,v2), ..., ?(Sj,vl), ...,
?(Sj,vp), are in one block of partition ?i. A
sufficient and necessary condition of existence
of decomposition of automaton M, with an
autonomous clock with ?log2?(?)? states is that
there exists a closed partition ? and a
non-trivial, compatible with input partition ?i
of the set of states S of this machine such that
? ? ?i