PRODUCTS OF INERTIA

1
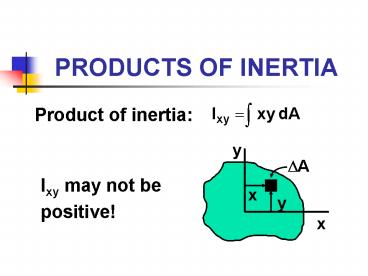
PRODUCTS OF INERTIA

• Product of inertia

Ixy may not be positive!
2
The Rectangle

• Compute Ixy. dA dxdy
• dIxy xydxdy

3
Geometrical Meaning

• Product of inertia

Ixy 0
Ixy 0
Ixy h2b2/2
4
Parallel Axis Theorem

• Virtually the same as for Ix, Iy.

5
Principal Axes Principal Moments of Inertia

• Consider

referred to coordinate system x,y
6
Motivation

• The Rectangle

Ix bh3/12
Iy hb3/12
Ix hb3/12
Iy bh3/12
Ix, Iy, Ixy values change when axes are rotated!
7
Problem 1

• How does I change when we refer it to a rotated
  set of axes x,y, i.e., how are Ix , Iy ,
  Ixy related to Ix , Iy , Ixy?

8
Coordinate Transformation

• The coordinates of a point P in the x,y system
  and the x,y system are related by

x xcosq ysinq y ycosq - xsinq
9
Transformation of Moments of Inertia

• Recall

y ycosq - xsinq
10
more

• Final form

Note Ix Iy Ix Iy
11
The Rectangle

• Note

Ix bh3/12 Iy hb3/12 Ixy 0
12
Problem 2

• What is the orientation of axes x,y which give
  extremal values of 2nd moment? What are those
  values?

13
Principal Values, Axes

• Extrema

?
2 values of 2q 180O apart.
2 values of q 90O apart.
2 values of q are principal axes
14
more

• Recall

Ixy 0 products of inertia vanish !
?
Ix - (IxIy) /22 Ixy2 (Ix-Iy) /22
Ixy2
Principal values !
15
Summary

• Values referred to rotated axes
• Principal axes, values