Presentazione di PowerPoint

1
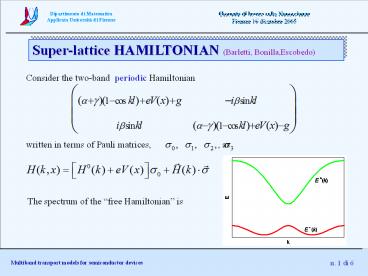
Super-lattice HAMILTONIAN (Barletti,
Bonilla,Escobedo)
Consider the two-band periodic Hamiltonian
written in terms of Pauli matrices,
, as
The spectrum of the free Hamiltonian is
2
Wigner spinorial functions

• We decompose the Wigner matrix
  in terms of Pauli matrices

where

• The expected value of the observable
  when system is at the state is given
  by integration over the phase-space of the
  following function

• Electron densities in the band at time t

3

• The evolution equations for the Wigner functions

where
is the pseudo-differential operator
are the Wigner functions at local equilibrium,
written in terms of Fermi-Dirac distributions
for the two bands, as function of the two band
densities
4
CHAPMAN-ENSKOG expansion
SCALING

• Hyperbolic scaling potential and collisions are
  dominant
• Weak coupling is small with respect to

We define the moment operators band densities
Chapman-Enskog ansatz
5
Then
We obtain a hierarchy of equations for
Expanding up to the order m1, we can write
explicitly
6
Drift-diffusion equations
QDD
where
is the generation-recombination operator
etc., etc.