The Unit Circle

1
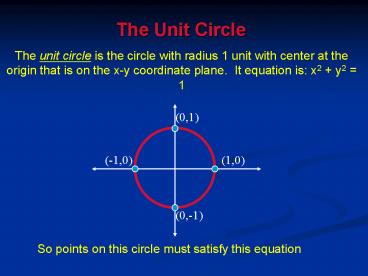
The Unit Circle
The unit circle is the circle with radius 1 unit
with center at the origin that is on the x-y
coordinate plane. It equation is x2 y2 1
So points on this circle must satisfy this
equation
2
The Unit Circle
What is the y coordinate of the point that lies
on the unit circle with x- coordinate ½ ?
x 1/2
(0,1)
ö
æ
3
1

ç
,

ç
2
2
ø
è
(1,0)
(-1,0)
ö
æ
3
1

ç
-
,

ç
(0,-1)
2
2
ø
è
3
Terminal Points on the Unit Circle
Let's say that we wanted to mark off a distance t
along the unit circle. We can start at the point
(1,0) and move counterclockwise if t is positive,
and clockwise if t is negative. The position P
(x,y) where you end up is known as the TERMINAL
POINT DETERMINED BY THE REAL NUMBER t.
t gt 0
P (x, y)
A (1, 0)
A (1, 0)
t lt 0
P (x, y)

1. For any real number t, there is a point P on the
   unit circle, such that the length of the arc AP
   where A is the point (1,0) and P is the
   terminating point is t.
2. Since the circumference of the unit circle is 2 p
   we see that t lt 2 p  
3. Hence we get a one-to-one correspondence between
   the real numbers in the interval 0, 2 p ) and
   the points on the unit circle.

4
Terminal Points on the Unit Circle

t Terminal Point Determined by t
0, 2p (1,0)
p/6 (v3/2, ½)
p/4 (v2/2, v2/2)
p/3 (½, v3/2)
p/2 (0,1)
5
The Unit Circle
Here is the unit circle divided into 8 pieces.
(0,1)
90
(v2/2, v2/2 )
(- v2/2, - v2/2 )
135
These are easy to memorize since they all have
the same value with different signs depending on
the quadrant.
45
45
180
(1,0)
(-1,0)
0
225
315
(v2/2, -v2/2 )
(- v2/2, - v2/2 )
270
(0,-1)
6
(0, 1)
What are the coordinates of this point?
30º
(1, 0)
(1, 0)
(0, 1)
7
(0, 1)
What are the coordinates of this point?
45º
(1, 0)
(1, 0)
(0, 1)
8
Reference Numbers
Due to the symmetries of the unit circle, to find
a terminal point in any quadrant, we only need to
know the "corresponding" terminal point in the
first quadrant. The reference number t is the
shortest distance along the unit circle between
the terminal point determined by t and the x -
axis. To find the reference number use the
following steps Step 1 identify the quadrant
the terminal point lies in Step 2 Find the
reference number t. Step 3 Find the terminal
point Q(x,y) determined by t. Step 4 The
terminal point determined by t is P( x, y),
where the signs are chosen according to the
quadrant in which this terminal point lies.
9
Trigonometric Functions of Real Numbers
The position P (x,y) where you end up is known as
the TERMINAL POINT DETERMINED BY THE REAL NUMBER
t.

• Note that the arc AP (s ? since r1) subtends
  a central angle.
• And on the unit circle, the measure of a central
  angle and the length of
• its arc are represented by the same real
  number t.

10
Trigonometric Functions of Real Numbers
The trigonometric functions of a real number are
defined in terms of x, y and r
11
Trigonometric Functions of Real Numbers
Let t be any real number and let P(x, y) be t he
terminal point on the unit circle determined by
t. These trigonometric functions of the real
number t are defined as sin t y cos t x
tan t y / x (x?0) csc t 1/ y (y?0) sec t
1/x (x?0) cot t x / y (y?0)
12
Recall Trigonometric Functions of Angles
13
Signs of Trigonometric Functions
sin csc are positive in Quadrant II
All are positive in Quadrant 1
tan cot are positive in Quadrant III
cos sec are positive in Quadrant IV
14
Signs of Trigonometric Functions
All
Students
Take
Calculus
15
(No Transcript)
16
The Graph of y sin x
17
Characteristics of the Sine Function

1. Domain is the set of all real numbers.
2. Range is all real numbers from -1 to 1, inclusive
3. It is symmetric with the origin (ODD Function
   which means f(-x) -f(x))
4. The sine function is periodic with period 2p so
   sin (t 2 p) sin (t)
5. The x intercepts are -2 p, - p, 0 , p, 2 p
6. The y-intercept is 0

18
The Graph of y cos x

1. Domain is the set of all real numbers.
2. Range is all real numbers from -1 to 1,
   inclusive
3. It is symmetric with the y-axis so it is an
   EVEN Function which means f(-x) f (x)
4. The cosine function is periodic with period 2p
   so cos (t 2 p) cos(t)
5. The x intercepts are - p/2, p/2 , 3p/ 2 ,
   5p/2
6. The y-intercept is 1

19
Graphing Trig Functions