Composite Quadrature

1
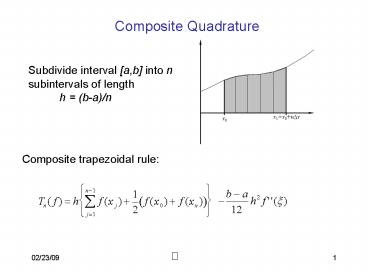
Composite Quadrature
Subdivide interval a,b into n subintervals of
length h (b-a)/n
Composite trapezoidal rule

2
Recursive Quadrature
Subdivide the interval a,b into 2k-1 equal
parts (k1, 2,)
and replace n --gt 2k-1 and use hk
(b-a)/2k-1
Rk,1 denotes the result of applying the composite
trapezoid rule with 2k-1 equal subintervals.

3
Recursive Quadrature
For example R3,1 uses the values of f at five
points a, a(b-a)/4, a2(b-a)/4,
a3(b-a)/4, b
For R4,1 we need values of f at 9 points a,
a(b-a)/8, a2(b-a)/8, a3(b-a)/8, .,
a7(b-a)/8, b
For R4,1 we need values of f at the 5 points used
for R3,1 plus four new additional points.

4
Recursive Quadrature
If Rk-1,1 has been calculated we can write Rk,1 as
Calculate the expression in the brackets with as
little additional work as possible!

5
Recursive Quadrature
Thus for the term in the brackets
Each term in the first sum that corresponds to an
even value of i is canceled out by a term in the
second sum.

6
Recursive Quadrature
Recursive Trapezoid Formula
If Rk-1,1 is available, then Rk,1 can be
recursively computed
Allows to compute a sequence of approximations to
a definite integral using the trapezoidal rule
without reevaluating the integrant at points
where it has already been evaluated.

7
PROGRAM CTR IMPLICIT NONE REAL
A, B, RK1 INTEGER K INTEGER,
PARAMETER KMAX 20 INTERFACE SUBROUTINE
TRAPEZOID (A, B, RK1, K) IMPLICIT NONE
INTEGER, INTENT(IN) K REAL,
INTENT(IN) A, B REAL,
INTENT(IN OUT) RK1 END SUBROUTINE
TRAPEZOID END INTERFACE A 0. B 1. DO K 1,
KMAX CALL TRAPEZOID(A, B, RK1, K) WRITE
(,) K, RK1 END DO STOP END PROGRAM CTR

8
Test to decide if subintervals should be further
divided
PROGRAM CTR IMPLICIT NONE REAL
OLDRK1 -1.E30 REAL,
PARAMETER EPS 1.E-5 INTEGER,
PARAMETER KMAX 20 .. DO K1,KMAX CALL
TRAPEZOID(A,B,RK1,K) WRITE(,) K,RK1 IF (K
.GT. 5) THEN IF (ABS(RK1 - OLDRK1) . LT.
EPSABS(OLDRK1) .OR. ((RK1 .EQ. 0) .AND.
(OLDRK1 .EQ. 0))) EXIT END IF OLDRK1
RK1 END DO STOP END PROGRAM CTR

9
Some built in flexibility
SUBROUTINE TRAPEZOID ( A, B, RK1, K) IMPLICIT
NONE INTEGER, INTENT(IN) K REAL,
INTENT(IN) A, B REAL,
INTENT(IN OUT) RK1 INTEGER IT,
I REAL SUM, HK, X IF (K .EQ. 1)
THEN f(a) and f(b) appear here ELSE
fa(2i-1)hk need to be called here END
IF RETURN END SUBROUTINE TRAPEZOID
We can hardwire the calls to the function f
or we can make our program more flexible!

10
or we can make our program more flexible!
SUBROUTINE TRAPEZOID (A, B, RK1, K) IMPLICIT
NONE INTERFACE FUNCTION FUNC (X)
IMPLICIT NONE REAL
FUNC REAL, INTENT(IN) X END FUNCTION
FUNC END INTERFACE IF (K.EQ.1) THEN Call to
FUNC(A) and FUNC(B) ELSE Call to
FUNC(A(2I-1)HK)) END IF RETURN END SUBROUTINE
TRAPEZOID
FUNCTION FUNC (X) IMPLICIT NONE REAL
FUNC REAL, INTENT(IN) X FUNC
4./(1.X2) RETURN END FUNCTION FUNC

11
Recursive Quadrature
Example of Recursive Trapezoid Formula
Convergence is quite slow. Next, we improve the
convergence using the Romberg Integration Method
R(2,1) 0.94805945
R(3,1) 0.98711580 R(4,1) 0.99678517 R(5,1) 0
.99919668 R(6,1) 0.99979919 R(7,1) 0.99994980
R(8,1) 0.99998745

12
Romberg Integration
Romberg integration uses the recursive trapezoid
rule with successively halved step sizes.
Recall that the error term in the composite
trapezoid formula is given by
In Romberg integration, we eliminate some of the
error terms to increase the rate of convergence.

13
Romberg Integration
Lets replace the index k with k1 (which means
that we double the number of subintervals).
The new stepsize will hk1 hk/2
Multiply by 4 and subtract it from the equation
at the top.

--gt h2-term will drop out
14
Romberg Integration

15
Romberg Integration
Thus a new approximation for our integral would
be
Repeat the procedure by calculating the integral
with Rk1,2
Multiplying by 16 and subtract it from the
equation at top.

--gt h4-term will drop out
16
Romberg Integration
Thus a new approximation for the integral is
If we repeat this procedure over and over again,
we find the general recursive formula
and an approximation for the integral is

17
Romberg Integration
The results of this algorithm can be tabulated as

18
Romberg Integration
The results of this algorithm can be tabulated as

19
Romberg Integration
The results of this algorithm can be tabulated as

20
Romberg Integration
The results of this algorithm can be tabulated as

21
Romberg Integration
The results of this algorithm can be tabulated as
Only the first column in the table requires an
evaluation of the integrant function using the
composite trapezoid rule (CTR).

Entire new row can be calculated from one
additional CTR.
22
Romberg Integration
Two options to generate the Romberg table

• Computer a reasonable number of terms for the
• first column Rk,1, and then use the
  extrapolation formula to construct the the
  columns 2, 3 ,, n in order.

2. Computer the table row by row. For
example, R2,2 can be computed as soon as R1,1 and
R2,1 are available

23
PROGRAM ROMBERG IMPLICIT NONE REAL .. INTERFACE
SUBROUTINE TRAPEZOID (A, B, RK1, K) ..
END SUBROUTINE TRAPEZOID END INTERFACE A 0. B
1. DO K 1, KMAX CALL TRAPEZOID(A, B, RK1,
K) .. DO J 2, K Use Romberg Formula
.. END DO .. WRITE (,) K,
R(K,K) END DO STOP END PROGRAM ROMBERG
PROGRAM CTR IMPLICIT NONE REAL
A, B, RK1 INTEGER K INTEGER,
PARAMETER KMAX 20 INTERFACE SUBROUTINE
TRAPEZOID (A, B, RK1, K) IMPLICIT NONE
INTEGER, INTENT(IN) K REAL,
INTENT(IN) A, B REAL,
INTENT(IN OUT) RK1 END SUBROUTINE
TRAPEZOID END INTERFACE A 0. B 1. DO K 1,
KMAX CALL TRAPEZOID(A, B, RK1, K) WRITE (,)
K, RK1 END DO STOP END PROGRAM CTR

24
Romberg Integration
Example of Romberg Integration
Lets use the same example as before
With the composite trapezoid rule we had already
calculated the first row (R1,1) for our Romberg
table.
Using the first 5 values, we get
1.00000001 1.00000000
1.00000000
0.78539816 0.94805945 0.98711580 0.99678517 0.9991
9668
1.00227988 1.00013458 1.00000830 1.00000052
0.99999157 0.99999988 1.00000000