Example: Manufacturing Integrated Circuits

1
Example Manufacturing Integrated Circuits
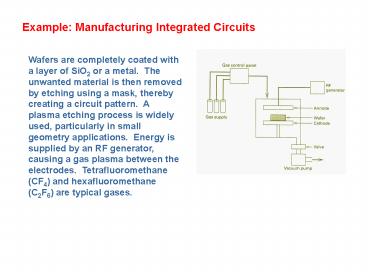
Wafers are completely coated with a layer of SiO2
or a metal. The unwanted material is then
removed by etching using a mask, thereby creating
a circuit pattern. A plasma etching process is
widely used, particularly in small geometry
applications. Energy is supplied by an RF
generator, causing a gas plasma between the
electrodes. Tetrafluoromethane (CF4) and
hexafluoromethane (C2F6) are typical gases.
2
Example Manufacturing Integrated Circuits
Wafers are completely coated with a layer of SiO2
or a metal. The unwanted material is then
removed by etching using a mask, thereby creating
a circuit pattern. A plasma etching process is
widely used, particularly in small geometry
applications. Energy is supplied by an RF
generator, causing a gas plasma between the
electrodes. Tetrafluoromethane (CF4) and
hexafluoromethane (C2F6) are typical gases.
An engineer is interested in testing the
relationship between the RF power setting and the
etch rate in this process.
3
Example Manufacturing Integrated Circuits
Wafers are completely coated with a layer of SiO2
or a metal. The unwanted material is then
removed by etching using a mask, thereby creating
a circuit pattern. A plasma etching process is
widely used, particularly in small geometry
applications. Energy is supplied by an RF
generator, causing a gas plasma between the
electrodes. Tetrafluoromethane (CF4) and
hexafluoromethane (C2F6) are typical gases.
An engineer is interested in testing the
relationship between the RF power setting and the
etch rate in this process. She decides to use
C2F6 gas and to test two power levels 160 W and
180 W, with 5 repeats of each.
4
(No Transcript)
5
One way to get a random test sequence the 10
power values were entered in an Excel
spreadsheet, a random number was generated for
each, and then the random numbers were ordered.
6
Etch Rate data ( Å/min.) from the plasma etching
experiment
7
Etch Rate data ( Å/min.) from the plasma etching
experiment
Is the difference between the mean etch rates
significant?
8
530
550
570
590
610
9
530
550
570
590
610
10
s160 20 Å/min s180 16 Å/min S160 20.0
Å/min S180 16.7 Å/min
For 5 values per set, these appear normal and we
could say s160 s180
530
550
570
590
610
11
Hypotheses H0 µ180 µ160 H1 µ180 gt µ160
12
Hypotheses H0 µ180 µ160 H1 µ180 gt
µ160 Using the appropriate t-Test, if t0 gt ta,v
with v 8. If a 0.05 then H0 is rejected with
5 error probability (that it is true).
13
ta,v t0.05, 8 1.860 and 3.10 gt 1.86 so H0 is
rejected. In fact, if we had chosen a 0.01,
then ta,v t0.01, 8 2.896 and H0 would still
be rejected. We can be confident, to an error of
1, that the etching rate at 180 W is greater
than that at 160 W.
14
ta,v t0.05, 8 1.860 and 3.10 gt 1.86 so H0 is
rejected. In fact, if we had chosen a 0.01,
then ta,v t0.01, 8 2.896 and H0 would still
be rejected. We can be confident, to an error of
1, that the etching rate at 180 W is greater
than that at 160 W.
But what if the engineer had been more
ambitiousif she had taken power data at
different power readings? 160 W, 180 W, 200 W,
220 W?
15
(No Transcript)
16
Here are the means for the augmented data. What
types of analysis can we do?
17
Box plots and a scatter diagram of the etch rate
data
18
Box plots and a scatter diagram of the etch rate
data
What else? Anything more quantifiable?
19
Can we do a t-Test or t-Tests?
20
Can we do a t-Test or t-Tests? No, pair-wise
comparison will give an inflated a error
21
The appropriate procedure for testing the
equality of several means is the analysis of
variance ANOVA. ANOVA has a wide application
(wider than this problem)it is probably the most
useful technique in the field of statistical
inference.
22
The appropriate procedure for testing the
equality of several means is the analysis of
variance ANOVA. ANOVA has a wide application
(wider than this problem)it is probably the most
useful technique in the field of statistical
inference.
Lets start out by assuming that we have a
treatments or different levels of a single factor
(e.g., 4 treatments of electrical power or 2
treatments of mortar). For each treatment lets
assume there will be n observations or samples.
23
The appropriate procedure for testing the
equality of several means is the analysis of
variance ANOVA. ANOVA has a wide application
(wider than this problem)it is probably the most
useful technique in the field of statistical
inference.
Lets start out by assuming that we have a
treatments or different levels of a single factor
(e.g., 4 treatments of electrical power or 2
treatments of mortar). For each treatment lets
assume there will be n observations or samples.
So there are i treatments (i 1a) with each
treatment having n repetitions.
The mean of the ith treatment
(j indexes the repetitions)
24
Repetitions
j 1 2 3 4 5 6
i 1 2 3 4 5 6 7 . .
Treatments
25
Repetitions
j 1 2 3 4 5 6
i 1 2 3 4 5 6 7 . .
Treatments
Just two treatments to comparethen we can use a
simple comparative test, such as the t-Test.
26
Repetitions
j 1 2 3 4 5 6
i 1 2 3 4 5 6 7 . .
Treatments
Just two treatments to comparethen we can use a
simple comparative test, such as the t-Test.
27
Repetitions
j 1 2 3 4 5 6
i 1 2 3 4 5 6 7 . .
Treatments
Just two treatments to comparethen we can use a
simple comparative test, such as the t-Test.
28
Repetitions
j 1 2 3 4 5 6
i 1 2 3 4 5 6 7 . .
Treatments
But to compare all of them at oncewe need a new
test.
29
The hypotheses we are interested in are H0 µ1
µ2 µa H1 µi ? µj for at least one pair
(i, j)
30
The hypotheses we are interested in are H0 µ1
µ2 µa H1 µi ? µj for at least one pair
(i, j) The ith mean treatment can be expressed
in terms of the overall mean (all treatments) and
a treatment factor µi µ Ti .
31
The hypotheses we are interested in are H0 µ1
µ2 µa H1 µi ? µj for at least one pair
(i, j) The ith mean treatment can be expressed
in terms of the overall mean (all treatments) and
a treatment factor µi µ Ti . Then since
32
an equivalent way to right the hypotheses is
then H0 T1 T2 Ta 0 H1 Ti ? 0
for at least one i We can either speak of testing
the equality of treatment means or testing that
the treatment effect (the Ti) are zero.
33
an equivalent way to right the hypotheses is
then H0 T1 T2 Ta 0 H1 Ti ? 0
for at least one i We can either speak of testing
the equality of treatment means or testing that
the treatment effect (the Ti) are zero. A new,
expanded definition of the F-test is used to
check whether to accept or reject the null
hypothesis (H0). Recall, we last saw the F-test
when we were comparing variances of just two
samples. Back then the test statistic was
34
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
35
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
If there are no differences in the treatment
means, these two variability estimates should be
very similar if they are not, then we should
suspect that the observed differences must be
caused by differences in the treatments.
36
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
If there are no differences in the treatment
means, these two variability estimates should be
very similar if they are not, then we should
suspect that the observed differences must be
caused by differences in the treatments.
j 1 2 3 4 5 6
If treatments make no difference, it doesnt
matter how we choose a sample to estimate
variance.
i 1 2 3 4
37
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
If there are no differences in the treatment
means, these two variability estimates should be
very similar if they are not, then we should
suspect that the observed differences must be
caused by differences in the treatments.
j 1 2 3 4 5 6
If treatments make no difference, it doesnt
matter how we choose a sample to estimate
variance.
i 1 2 3 4
38
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
If there are no differences in the treatment
means, these two variability estimates should be
very similar if they are not, then we should
suspect that the observed differences must be
caused by differences in the treatments.
j 1 2 3 4 5 6
If treatments make no difference, it doesnt
matter how we choose a sample to estimate
variance.
i 1 2 3 4
39
Now we are testing the variances of many
treatments, and the expanded test statistic is a
ratio
If there are no differences in the treatment
means, these two variability estimates should be
very similar if they are not, then we should
suspect that the observed differences must be
caused by differences in the treatments.
j 1 2 3 4 5 6
If treatments make no difference, it doesnt
matter how we choose a sample to estimate
variance.
i 1 2 3 4
40
Before continuing, a note about the dot
subscript notation
41
Before continuing, a note about the dot
subscript notation
With these definitions,
42
Generally, if this new F0 is near one then the
treatments make no difference, and we cannot
reject the null hypothesis, H0 µ1 µ2 µa
. If this F0 is far from 1 then there is likely a
significant difference between at least two
treatments, and we can reject the null
hypothesis.
43
Generally, if this new F0 is near one then the
treatments make no difference, and we cannot
reject the null hypothesis, H0 µ1 µ2 µa
. If this F0 is far from 1 then there is likely a
significant difference between at least two
treatments, and we can reject the null
hypothesis. Formally,
where
44
and
with
45
We should reject the null hypothesis and conclude
that there are differences in treatment means if
where Fa, a-1, N-a is an F-distribution
percentage with (a-1) and (N-a) degrees of
freedom.
46
We should reject the null hypothesis and conclude
that there are differences in treatment means if
where Fa, a-1, N-a is an F-distribution
percentage with (a-1) and (N-a) degrees of
freedom.
Lets apply this procedure and test statistic to
the engineering example we started with.
47
(No Transcript)
48
(No Transcript)
49
Now we can apply ANOVA Analysis of Variance to
test the mean etch rates at different power
settings, H0 µ160 µ180 µ200 µ220 (a 4,
n 5) against the alternate H1.
50
Now we can apply ANOVA Analysis of Variance to
test the mean etch rates at different power
settings, H0 µ160 µ180 µ200 µ220 (a 4,
n 5) against the alternate H1.
51
So,
The F-Test for rejecting H0 is, So, if a 0.05
then this becomes
52
The test is fulfilled and we are justified in
rejecting H0there is enough variance in the
samples to say, to within a 0.05, that there is
a significant difference between the mean etch
rates. Even if a 0.01, the test is met
53
The test is fulfilled and we are justified in
rejecting H0there is enough variance in the
samples to say, to within a 0.05, that there is
a significant difference between the mean etch
rates. Even if a 0.01, the test is met
In fact, a could be as small as 2.88 10-9 and
H0 would still be rejected. That is, the P-value
is P 2.88 10-9.