Sequencing Methods

1
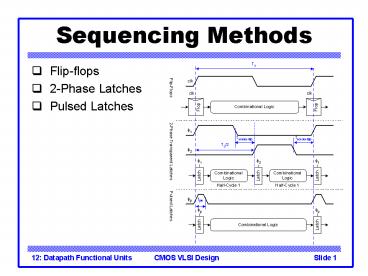
Sequencing Methods

• Flip-flops
• 2-Phase Latches
• Pulsed Latches

2
Timing Diagrams
Contamination and Propagation Delays
3
Max-Delay Flip-Flops
tpcq tpd tsetup lt Tc
_
or
4
Max Delay 2-Phase Latches

• Assuming a single cycle path

tpdq1 tpd1 tpdq2 tpd2 lt Tc
_
or
5
Max Delay Pulsed Latches

• Wide pulse (tpw gt tsetup)

tpdq tpd lt Tc
_

• Narrow pulse (tpw lt tsetup)

tpcq tpd tsetup tw lt Tc
_
6
Min-Delay Flip-Flops
tccq tcd gt thold
_
or
7
Min-Delay 2-Phase Latches
tnonoverlap tccq tcd gt thold
_
or

• Non-overlapped clocking scheme helps meeting hold
  time requirements

8
Min-Delay Pulsed Latches
tccq tcd gt thold tpw
_
or

• Hold time increased by pulse width

9
Time Borrowing

• In a flop-based system
• Data launches on one rising edge
• Must setup before next rising edge
• If it arrives late, system fails
• If it arrives early, time is wasted
• Flops have hard edges
• In a latch-based system
• Data can pass through latch while transparent
• Long cycle of logic can borrow time into next
• As long as each loop completes in one cycle

10
Time Borrowing Example
11
How Much Borrowing?
2-Phase Latches
Without borrowing
tpd lt Tc/2 - tpdq
_
With borrowing
Toverlap tsetup tborrow lt Tc/2
_
or

• Use intentional time borrowing wisely

12
Clock Skew

• We have assumed zero clock skew
• Clocks really have uncertainty in arrival time
• Reduces maximum propagation delay available for
  logic to meet set-up time requirements
• Increases minimum contamination delay required by
  logic to meet hold time requirements
• Reduces time borrowing

13
Skew Flip-Flops
14
Skew Latches

• 2-Phase Latches
• clock skew does not degrade set-up performance
• Increases hold time in each cycle

15
Solutions for set-up and Hold-time Violations

• If setup times are violated, reduce clock speed
• Often clock speed is fixed gt redesign logic in
  the critical path. Also, use clock borrowing (but
  not indiscriminately)
• If hold times are violated, chip fails at any
  speed
• hold time is independent of frequency
• Can add buffers in the data path to slow data
• An easy way to guarantee hold times is to use
  2-phase latches with big nonoverlap times, but
  2-phase clocking
• increases area
• May not be available in some cases

16
Safe Flip-Flop

• In class, use flip-flop with nonoverlapping
  clocks
• Very slow nonoverlap adds to setup time
• But no hold times
• In industry, use a better timing analyzer
• Add buffers to slow signals if hold time is at
  risk

17
Summary

• Flip-Flops
• Very easy to use, supported by all tools
• 2-Phase Transparent Latches
• Lots of skew tolerance and time borrowing
• Pulsed Latches
• Fast, some skew toler. borrow, hold time risk

18
Metastability

• When the set-up or hold time is violated, the
  latch or flip-flop can become metastable
• Delay increases and output becomes indeterminate
  for some time before settling to a known value
• Synchronizer
• Use back-to-back flip flops to transfer single
  bit signals between asynchronous clock domains
• For buses
• Use hand-shaking
• Gray coding
• FIFOs

19
Lecture 8 Datapath Functional Units
20
Outline

• Comparators
• Shifters
• Multi-input Adders
• Multipliers

21
Comparators

• 0s detector A 00000
• 1s detector A 11111
• Equality comparator A B
• Magnitude comparator A lt B

22
1s 0s Detectors

• 1s detector N-input AND gate
• Requires large fan-in gt use a tree of NAND2/NOR2
  gates (log N stages)
• 0s detector N-input NOR gates
• Requires large fan-in gt use a tree

DeMorgans Law
23
Equality Comparator

• Can be best implemented using EXNOR2 gates and a
  1s detector
• Check if each bit is equal (XNOR, aka equality
  gate)
• 1s detect on bitwise equality

24
Magnitude Comparator

• Compute B-A and look at sign
• B-A B (A 1)
• For unsigned numbers, carry out is sign bit

_
25
Signed vs. Unsigned

• For signed numbers, comparison is harder
• C carry out
• Z zero (all bits of A-B are 0)
• N negative (MSB of result)
• V overflow (inputs had different signs, output
  sign ? B)

26
Shifters

• Logical Shift
• Shifts number left or right and fills with 0s
• 1011 LSR 1 0101 1011 LSL1 0110
• Arithmetic Shift
• Shifts number left or right. Rt shift sign
  extends
• 1011 ASR1 1101 1011 ASL1 0110
• Rotate
• Shifts number left or right and fills with lost
  bits
• 1011 ROR1 1101 1011 ROL1 0111

27
Funnel Shifter

• A funnel shifter can do all six types of shifts
• Selects N-bit field Y from 2N-bit input
• Shift by k bits (0 ? k lt N)

28
Funnel Shifter Operation

• Computing N-k requires an adder

29
Funnel Shifter Operation

• Computing N-k requires an adder

30
Funnel Shifter Operation

• Computing N-k requires an adder

31
Funnel Shifter Operation

• Computing N-k requires an adder

32
Funnel Shifter Operation

• Computing N-k requires an adder

33
Simplified Funnel Shifter

• Optimize down to 2N-1 bit input

34
Funnel Shifter Design 1

• An array of N N-input multiplexers (each row
  forms a Mux)
• Use 1-of-N hot select signals for shift amount
• One Mux for each output bit (horizontal)
• Only one select signal is high in each case
• nMOS pass transistor design (Vt drops!)

Pass transistor stick Diagram
35
Funnel Shifter Design 2

• Log N stages of 2-input muxes
• No select decoding needed

36
Multi-input Adders

• Suppose we want to add k N-bit words
• Ex 0001 0111 1101 0010 10111
• Straightforward solution k-1 N-input CPAs (Carry
  propagation Adders)
• But is large and slow

37
Carry Save Addition

• A full adder sums 3 inputs and produces 2 outputs
• Carry output has twice weight of sum output
  because carry is added to the next MSB bit
• N full adders in parallel are called carry save
  adder
• Produce N sums and N carry outs

38
CSA Application

• Use k-2 stages of CSAs
• Keep result in carry-save redundant form (carry
  outputs are preserved rather than propagated)
• Final CPA computes actual result

39
Multiplication

• Example
• M x N-bit multiplication
• Produce N M-bit partial products by logical
  ANDing of the appropriate bits
• Sum these to produce MN-bit product

40
General Form

• Multiplicand Y (yM-1, yM-2, , y1, y0)
• Multiplier X (xN-1, xN-2, , x1, x0)
• Product

41
Dot Diagram

• Multiplication can be best illustrated using a
  dot diagram
• Each dot represents a 0/1 bit
• Horizontal boxes represent shifted partial
  products
• Multiplier bits on the right
• Using N-1 CPAs to add the partial products is
  slow

42
Array Multiplier

• 4x4 array multiplier for unsigned numbers using
  an array of CSAs
• First row converts the first
• partial product into carry
• save redundant form
• Each later row uses the
• CSA to add the corresponding
• partial product to the carry-
• save redundant result of the
• previous row
• The least significant N output
• bits are available as CSA sum
• outputs
• The MSB output bits require a
• 4 bit CPA to convert carry-sum
• form to regular binary

43
Rectangular Array

• Squash array to fit rectangular floorplan