Approximation methods in Quantum Mechanics

1
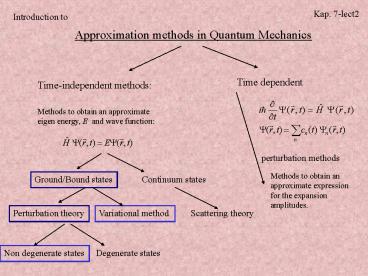
Approximation methods in Quantum Mechanics
Kap. 7-lect2
Introduction to
Time dependent
Time-independent methods
Methods to obtain an approximate eigen energy, E
and wave function
perturbation methods
Methods to obtain an approximate expression for
the expansion amplitudes.
Ground/Bound states
Continuum states
Perturbation theory
Variational method
Scattering theory
Non degenerate states
Degenerate states
2
Summary!
Perturbation theory
Variational method
3
Example 3 He ground state - Variation vs. 1.
Order perturbation
Perturbation theory
0. Order
1. Order
4
Final 1. Order Result
Discuss H-, Li, etc!
5
Variational method
Reasonable Trial Function
Expectation value of Z
Minimization
2.68 for Z2
Final Result
6
Comparison - Example 3
Variational method
Perturbation theory
Experiment
7
Degenerate time independent perturbation theory
Assume the Hamiltonian can be written as a sum of
two parts
Assume
Insert
Rearrange
This is valid for all ms!
8
We obtain an eigenvalue problem for the energy
correction
Energy (The degeneracy is removed.)
0th order 1st order
9
Degenerate Example The Linear Stark effect.
Consider an excited n2 hydrogen atom, exposed to
a linear electric field
Unperturbed Hydrogen atom -gt
g4 -gt 1. St order energy correction from
Even/Odd symmetry in the integrals
10
The degeneracy is partly removed
g4
Validity
11
Example 5 - Long range forces between atoms

• The fact that neutral atoms attract each other at
  long distances is a mystery in classical physics!

• If the entire human knowlegde should be packed
  into one sentence it should beMatter consists
  of atoms - which attract each other at long
  distances and repel at short distances
  R. P. Feynmann

12
Unperturbed state
Energy correction
0 (zero level)!
0 due to symmetry!
A similar treatment at short distances give the
Lennard-Jones potential
Comments Large betwen metals, smaller betwen
oxydes, small between inert atoms etc etc.
13
Approximation methods in Quantum Mechanics
Kap. 7-lect2
Introduction to
Time dependent
Time-independent methods
Methods to obtain an approximate eigen energy, E
and wave function
Golden Rule
perturbation methods
Methods to obtain an approximate expression for
the expansion amplitudes.
Ground/Bound states
Continuum states
Perturbation theory
Variational method
Scattering theory
Non degenerate states
Degenerate states