IP: Addresses and Forwarding PowerPoint PPT Presentation
Title: IP: Addresses and Forwarding
1
(No Transcript)
2
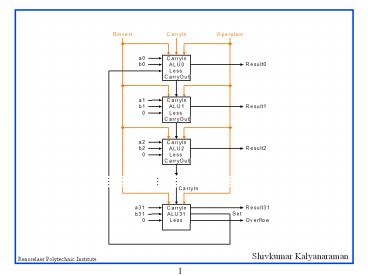
Problem ripple carry adder is slow
- Is a 32-bit ALU as fast as a 1-bit ALU?
- Is there more than one way to do addition?
- Two extremes ripple carry and sum-of-products
- c1 b0c0 a0c0 a0b0
- c2 b1c1 a1c1 a1b1
- c3 b2c2 a2c2 a2b2
- c4 b3c3 a3c3 a3b3
3
Carry-lookahead adder
- An approach in-between our two extremes
- More complexity (gates) vs less propagation
(levels) - Motivation
- If we didn't know the value of carry-in, what
could we do? - When would we always generate a carry? gi
ai bi - When would we propagate the carry? pi
ai bi - Rewriting the carry equations, we get
- c1 g0 p0c0
- c2 g1 p1c1 or c2
- c3 g2 p2c2 or c3
- c4 g3 p3c3 or c4
4
Carry-lookahead adder block
- Consider the equation for the last carry c4
- c4 g3 (p3.g2) (p3.p2.g1) (p3.p2.p1.g0)
- (p3.p2.p1.p0.c0), or .
- c4 G0 P0.c0, where
- G0 g3 (p3.g2) (p3.p2.g1) (p3.p2.p1.g0)
- P0 p3.p2.p1.p0
- Calling c4 as C1 and c0 as C0, we have C1 G0
P0.C0
5
Use principle to build bigger adders
- Use 4-bit ALU and a 4-bit CLA building blocks
- I.e., given Pi, Gi and C0, 4-bit CLA can find C1,
C2, C3, C4 in parallel! - Ripple is eliminated !
- Ripple carry speed
- (16 hops between 1-bit ALUs)
- (2 logic levels at each ALU)
- 32 gate delays
- CLA-adder speed
- (1 logic level to compute pi, gi)
- (2 logic levels to compute Pi, Gi from pi,gi)
- (2 logic levels at CLA to compute Ci)
- 5 gate delays !!
C
a
r
r
y
I
n
a
0
C
a
r
r
y
I
n
b
0
R
e
s
u
l
t
0
-
-
3
a
1
b
1
A
L
U
0
a
2
p
i
P
0
4-bit
b
2
g
i
G
0
a
3
b
3
C
a
r
r
y
-
l
o
o
k
a
h
e
a
d
u
n
i
t
C
1
c
i
1
C
a
r
r
y
I
n
a
4
b
4
R
e
s
u
l
t
4
-
-
7
a
5
b
5
A
L
U
1
a
6
p
i
1
P
1
b
6
g
i
1
G
1
a
7
b
7
C
2
c
i
2
C
a
r
r
y
I
n
a
8
b
8
R
e
s
u
l
t
8
-
-
1
1
a
9
b
9
A
L
U
2
a
1
0
p
i
2
P
2
b
1
0
G
2
g
i
2
a
1
1
b
1
1
C
3
c
i
3
C
a
r
r
y
I
n
a
1
2
b
1
2
R
e
s
u
l
t
1
2
-
-
1
5
a
1
3
b
1
3
A
L
U
3
a
1
4
p
i
3
P
3
g
i
3
G
3
b
1
4
a
1
5
C
4
c
i
4
b
1
5
C
a
r
r
y
O
u
t
PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.
You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.
About the Developers
PowerShow.com is brought to you by CrystalGraphics, the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.