Conecciones a travez del espacio

1

• Conecciones a travez del espacio
• Hasta ahora, todos los experimentos que
  analizamos
• funcionan por el acople escalar. COSY, HETCOR,
  HOMO-
• y HETERO2DJ, etc., etc., nos dan informacion
  sobre la
• estructura covalente del sistema, pero poco
  acerca de su
• conformacion o su estereoquimica (esto no es
  del todo cierto
• pero denme un poco de vida...).
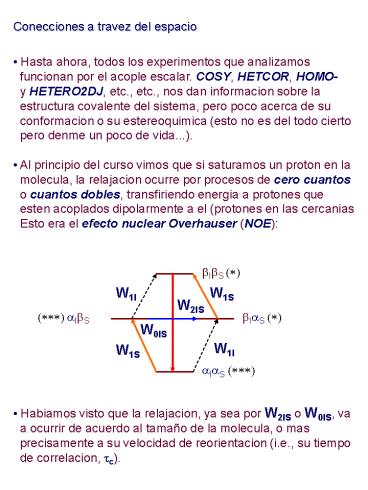
• Al principio del curso vimos que si saturamos un
  proton en la
• molecula, la relajacion ocurre por procesos de
  cero cuantos
• o cuantos dobles, transfiriendo energia a
  protones que
• esten acoplados dipolarmente a el (protones en
  las cercanias
• Esto era el efecto nuclear Overhauser (NOE)

bIbS ()
W1S
W1I
W2IS
() aIbS
bIaS ()
W0IS
W1I
W1S
aIaS ()
2

• Caso en un sistema de dos espines
• Habiamos establecido una relacion entre las
  velocidades de
• las distintas probabilidades y la magnitud del
  NOE. limitando
• todo a 1H-1H (gI / gS 1), tendremos
• fIS es el factor de NOE del nucleo I cuando
  saturamos al
• nucleo S. Esta ecuacion aparece de otra forma
  en muchos
• libros. Definimos la constante de ralajacion
  cruzada, sIS,
• como el numerador, y el denominador como la
  relajacion
• dipolar longitudinal, rIS.

W2IS - W0IS
hI fIS
2W1S W2IS W0IS
sIS W2IS - W0IS rIS 2W1S W2IS W0IS hI
sIS / rIS fIS
3

• Funciones de correlacion y densidad espectral
• Ya mencionamos que las rutas que el sistema
  tiene para
• liberar energia a la red dependen de las
  frecuencias de los
• distintos procesos que afectan al sistema.
• En solucion, esto significa rotacion de la
  molecula (tc). Los
• espines quedan alineados con el campo Bo
  externo mientras
• la molecula rota, y esto genera campos
  magneticos (dipolos
• fluctuantes) a la frecuencia de la rotacion que
  permiten que
• el sistema libere energia magnetica
• Tenemos que poder analizar como la molecula rota
  en
• solucion. Definimos la funcion de correlacion
  del sistema

g(t) R(t) R(t t)
4

• Densidad espectral
• Como ya sabemos, una vez que tenemos una funcion
  en el
• tiempo podemos ver las frecuencias de los
  procesos en
• cuestion haciendo una TF. La TF de g(t) se
  llama la funcion
• de densidad espectral, J(w). Como g(t) es una
  exponencial
• que decae en funcion de t, J(w) es una
  Lorentziana
• Dependiendo de tc (la modorra de la molecula),
  su
• movimiento esta compuesto por frecuencias mas
  lentas,
• comparables, o mas rapidas que wo, que es la
  frecuencia de
• Larmor del sistema

2 tc J(w) 1
w2tc2
wo
J(w)
wo tc gtgt 1 wo tc 1 wo tc ltlt 1
log(w)
5

• Todo junto
• Como la probablilidad de que una transicion
  ocurra depende
• de las distintas frecuencias que el sistema
  tenga (o densidad
• espectral), los terminos W son proporcionales a
  J(w).
• Igualmente, como se necesitan dos dipolos
  magneticos para
• tener acople dipolar, el NOE depende de la
  intensidad de los
• dipolos. Como la intensidad de un dipolo es
  proporcional a
• rIS-3, las probabilidades W van a depender de
  rIS-6

W0IS ? gI2 gS2 rIS-6 tc / 1 (wI -
wS)2tc2 W2IS ? gI2 gS2 rIS-6 tc / 1 (wI
wS)2tc2 W1S ? gI2 gS2 rIS-6 tc / 1
wS2tc2 W1I ? gI2 gS2 rIS-6 tc / 1 wI2tc2
6

• NOE estatico (steady-state)
• En moleculas rigidas chicas, las siguientes
  relaciones son
• validas
• Basicamente se mueven rapido. Los terminos en
  las
• equaciones de probabilidad (los Ws) se
  simplifican, y nos
• queda una relacion simple para el simple el
  NOE hI 0.5.
• Fenomeno, teniamos una dependencia con rIS-6
  pero
• desaparecio. El problema es que tenemos solo
  dos espines
• en el ejemplo, y esto quiere decir que no hay
  geometria.
• Esto es tipico para 1H-13C.

(wI - wS) tcltlt 1 wS tcltlt 1 wI tc ltlt 1 (wI
wS) tcltlt 1
b
a
c
rac
rba
7

• NOE estatico (continuado)
• Lo que sucede es que tenemos competencia entre
  los
• mecanismos de relajacion para el 1H que
  saturemos (dos o
• mas 1Hs en los alrededores). Las velocidades
  relativas de
• relajacion con respecto a distintos 1Hs son lo
  mportante en
• este caso (las respectivas Ws).
• Las ecuaciones se complican mas, pero si aun
  estamos en
• el extreme narrowing limit, se simplifican un
  monton. Al
• final, podemos establecer una relacion simple
  entre el NOE
• y las distancias interatomicas (1Hs en este
  caso...)

rIS-6 - SX fXS
rIX-6 fIS hmax
rIS-6 SX rIX-6
8

• Espectroscopia NOE de diferencia
• Si nuestra molecula tiene tres protones, dos de
  los cuales
• estan a una distancia fija (un CH2), tenemos
• Como tenemos dos protones de referencia (Ha y
  Hb) para
• los cuales sabemos la distancia, podemos
  definir un NOE
• de referencia y calcular la distancia entre
  otros protones

Hb
C
Hb
Ha
Hc
Ha
Hc
_

hab
hac
hab ? rab-6 rac rab ( hab / hac )
-1/6 hac ? rac-6
9

• NOE transitorio
• Uno de los problemas del NOE estatico es que le
  estamos
• dando energia al sistema continuamente
  (saturacion). Esto
• funciona bien para moleculas chicas, porque los
  procesos
• W2 (cuantos dobles) dominan (la molecula se
  mueve rapido).
• A medida que el tamaño y tc aumentan, otros
  procesos se
• vuelven mas importantes, como ser relajacion
  espin-espin
• (un cuanto) y transiciones prohibidas (cero
  cuantos).
• Ademas, hay mas protones en la vuelta y
  empezamos a ver
• un efecto llamado difusion de espines

I
S
10

• NOE transitorio (continuado)
• Ademas tenemos un monton de dificultades
  tecnicas cuando
• hacemos saturacion selectiva. Como lo que
  queremos es ver
• como el sistema vuelve al equilibrio por medio
  de ralajacion
• cruzada, podemos invertir selectivamente una
  transicion y
• observar como crece el NOE en funcion del
  tiempo
• Esta secuencia nos sirve

bIbS ()
W1S
W1I
W2IS
() aIbS
bIaS ()
W0IS
W1I
W1S
aIaS ()
90
180s
tm
inversion selectiva
11

• Noe transitorio (mas)
• Si lo hacemos a distintos valores de tm, nos dan
  curvas de
• crecimiento de NOE (NOE build-up curves), que
  en el caso
• de dos espines aislados y condiciones ideales
  nos da un
• crecimiento exponencial hasta llegar a hmax.
• Si tomamos en cuanta la relajacion T1 y T2, el
  NOE crece y
• despues decae a cero (toda la magnetizacion
  retorna al

hmax
tm
lt hmax
tm
12

• Ejemplo de NOESY-1D
• Estructura del acetato de
• trimetilpurpurogalina

(c
b)
a)
...o esta?
Esta...
c)
b)
a)
13

• NOE transitorio y NOESY
• Si tenemos mas espines y difusion de espines, la
  curva (para
• tres espines, I, S, y X) tendria esta
  apariencia
• Si queremos medir distancias con cierta
  precision, hay que
• que encontrar un compromiso entre el tiempo de
  mezcla tm
• que usemos y la difusion de espines que podamos
  tener.

hmax
Difusion a X
tm
90
90
90
t1
tm
inversion
14

• NOESY (continuado)
• Los primeros dos pulsos (con el tiempo t1
  variable) son una
• inversion para todos los protones en que
  marcamos todo
• con corrimientos quimicos y acoples (no hay
  reenfoque).
• Lo que termine en el eje -z evoluciona durante
  el periodo de
• mezcla tm, y los espines acoplados dipolarmente
  sufren
• relajacion cruzada (NOE) de acuerdo a las
  equaciones que
• vimos antes.
• El espectro despues del la TF 2D tiene
  corrimientos quimicos
• y acoples en f1 y en f2, y cross-peaks entre
  espines que
• esten dipolarmente acoplados

d (f1)
Hc
Hb
C
Ha
Ha
Hc
Hb
d (f2)
15

• NOESY (mas)
• Otra cosa que hay que considerar es el signo de
  los cross-
• peaks. Va a depender del tiempo de correlacion
  tc de la
• misma forma que los NOE en un 1D. Por lo tanto
  vamos a
• tener cross-peaks positivos para w tc ltlt 1 y
  negativos
• para w tc gtgt 1.
• Como vimos antes, hay un rango de valores de w
  tc para
• el cual el NOE puede ser cero. Si expresamos el
  NOE en
• funcion de w tc obtenemos una sigmoide, y si
  resolvemos
• para hI 0

16

• Trabajo a campos bajos - Spin-locking
• Hasta ahora, todos los experimentos han sido al
  campo
• magnetico del iman. Cuanto mas grande, mejor,
  ya que
• aumenta la sesibilidad y la resolucion.
• Hay algunos casos en que un campo mas chico
  (mucho mas
• chico) seria muy util. Por ejemplo, vimos que
  en ciertos casos
• tener un cierto campo Bo y una molecula con un
  tc en
• particular no nos permite usar NOESY (es cero).
• Idealmente querriamos tener la sensibilidad y
  resolucion que
• nos da Bo, pero estudiar el comportamiento del
  sistema de
• espines (transferencia de polarizacion,
  acoples, correlacion y
• relajacion cruzada, etc.) a otro campo.
• En un experimento 2D esto significa que los
  periodos de
• preparacion, evolucion, y adquisicion se llevan
  a cabo a Bo,
• pero el mezclado lo hacemos a un campo mas
  bajo.

17

• Teoria del Spin-locking
• Para tener spin-lock de la magnetizacion lo
  primero es
• sacarla del eje z (lejos de Bo). Esto quiere
  decir que la
• ponemos en los ejes x o y (i. e., un pulso p /
  2).
• Ahora viene la parte del enganche. Despues de
  que M este
• en el plano ltxygt, hay que mantenerla alli. Como
  dijimos,
• esto involucra hacerla precesionar alrededor de
  une nuevo
• campo magnetico alineado con el eje x o y.
• Esto lo hacemos con un campo de banda continua
  (BC) o
• con un campo generado por pulsos compuestos
  (tren de
• pulsos) que tiene el mismo efecto que la
  irradiacion de BC

z
z
90 BSL (x)
x
x
BSL
y
y
antes del SL wo g Bo despues del SL
wSL g BSL
18

• Teoria del Spin-locking (continuado)
• Tenemos que tener en cuenta que BSL es un campo
• magnetico variable aplicado en (o cerca de) la
  resonancia de
• los espines de nuestra muestra.
• Como es estatico en el sistema rotatorio, solo
  nos preocupa
• su intensidad. Por eso es que estos
  experimentos se
• conocen como experimentos de sistema rotatorio.
• Hay distintas formas de generar el BSL. Una es
  basicamente
• usar un campo de BC que prendemos y dejamos
  prendido
• por el tiempo que queramos los espines
  enganchados.
• El problema de esto es el ancho espectral que
  logramos
• con excitacion de BC. Solo los espines con wo
  similar a wSL
• van a estar bien enganchados. Para cubrir
  cosas a los
• costados hay que aumentar mucho la potencia.

wSL
19

• Spin-locking con MLEV
• Podemos usar pulsos de RF cortos y obtener los
  mismos
• resultados. Los llamamos pulsos compuestos, ya
  que son
• una coleccion de pulsos cortos (ms) esparcidos
  por todo el
• periodo de mezcla (o todo el periodo del
  spin-lock) y tienen el
• mismo efecto que irradiacion de BC.
• El mas comun es llamado MLEV, o ciclo de
  desacople de
• Malcom LEVitt. Una variacion es llamada DIPSI
• (Decoupling In the Presence of Scalar
  Interactions).
• Estas secuencias son esquemas de desacople
  (despues de
• todo, un BSL de BC es como un desacoplador), y
  tenemos
• que entender como funcionan los pulsos
  compuestos
• (PCs) para entender como logran el spin-lock.
• Un PC es basicmente un monton de pulsos juntos
  que
• usamos repetidas veces. PCs tipicos son R
  (p/2)x(p)y(p/2)x

z
z
R
x
x
y
y
20

• Spin-locking con MLEV (continuado)
• La cosa no termina aca. Tenemos que usar mas
  PCs para
• lograr el spin-lock. Si aplicamos el mismo
  pulso R
• Lo que hacen, basicamente, es mantener a la
  magnetication
• en el plano ltxygt tumbandola de un lado a otro a
  de los ejes.
• Si ponemos muchos en sucesion podemos mantener
  el
• spin-lock por el tiempo que queramos.
  Normalmente las
• fases de los distintos PCs del spin-lock se
  alternan (R)

z
z
R
x
x
y
y
_ _ _ _ _
_ _ _ MLEV-16 R R R R R R R R R
R R R R R R R
21

• TOCSY
• El largo y el tipo del spin-lock va a depender
  de lo que
• queramos hacer.
• La primera tecnica que vamos a analizar se llama
  HOHAHA
• (HOmonuclear HArtmann-HAhn experiment) o TOCSY
• (Total Correlation SpectroscopY). La utilidad
  de esta
• secuencia es identificar todos los epines en un
  sistema.
• Generalmente estudiamos acoples (en un 1D o en
  un COSY)
• bajo los efectos de Bo. Por lo tanto, Dd (Hz)
  gtgt J (Hz).
• Esto significa que los efectos en la energia del
  sistema
• debidos a los acoples (J) van a ser mucho
  menores que los
• efectos debidos a corrimientos quimicos (d), y
  la transferencia
• de energia entre distintos estados (coherencia)
  va a estar
• dominada por d. El sistema es de primer orden

H H? HJ con H? gtgt HJ
22

• TOCSY (continuado)
• Ahora el acople domina la energia del sistema, y
  la
• transferencia de coherencia ocurre debido al
  acople escalar.
• Para hacerla corta, vamos a tener un mezclado
  completo
• de los estados del sistema, y la coherencia de
  un espin en un
• sistema acoplado se transfiere a todos los
  otros espines. En
• otra palabras, un espin se correlaciona con
  todos los demas
• en el sistema
• La mayor transferencia entre dos espines con un
  acople de
• J Hz es optima cuando el periodo del spin-lock,
  tm, es 1 / 2J.
• tms mas largos nos dejan transferir coherencia
  en sistemas

A
B
C
X
D
tm
90s
23

• TOCSY (mas)
• Si hacemos el spin-lock
• en nucleos de distintos
• sistemas de espines en
• una molecular como
• esta nos daria
• Espin bajo spin-lock

B

C
A
B
A
C
24
Ejemplo de TOCSY-1D

• Soforolipido en estudio en el FDA de PA.
• Haciendo el spin-lock en los anomericos
• logramos identificar las dos glucosas...

Anomerico naranja
Anomerico verde

• Al lipido lo podemos identificar haciendo
  spin-locks en el
• metileno a al metilester, en el metilo, y en
  los olefinicos...

25

• TOCSY (y mas)
• Esto funciona bien para una molecula con pocos
  espines. El
• otro problema es que usamos pulsos selectvos,
  que nunca
• son tan selectivos como queremos.
• Usamos excitacion no selectiva (un pulso p / 2
  duro) en una
• tecnica 2D. La secuencia tiene esta apariencia
• Los dos pulsos antes y despues del mezclado son
  llamados
• pulsos de recorte (trimming pulses), y son
  necesarion para
• que el spin-lock funcione cuando usamos PCs
  con pulsos

90
90
90
t1
tm
26

• TOCSY (...y mas)
• SI graficamos el 2D vemos que todos los espines
  de un
• sistema en particular estan todos en una linea.
  Para el
• ejemplo anterior

d
27

• ROESY
• El otro experimento que usa un spin-lock es el
  ROESY
• (ROtating framE SperctroscopY), y es el
  equivalente
• en el sistema rotatorio del NOESY.
• Como vimos antes, el signo del NOE varia en
  funcion de
• w tc, y es cero para w tc 1.12.
• Si pudiesemos estudiar los acoples dipolares a
  campos
• mucho mas bajos que Bo no tenemos este problema
  porque
• w va a ser chiquita, y siempre estamos en el
  extreme
• narrowing limit donde todos los NOE son
  positivos

Bo - 100 a 800 MHz wSL ltlt wo w tc ltlt 1
BSL - 2 a 5 KHz
28

• ROESY (continuado)
• Como para todas las secuencias, hay un 1D y un
  2D. En el
• 1D usamos un pulso selectivo para afectar solo
  al espin para
• el que queremos medir efectos NOE
• Usando un pulso p / 2 no selectivo y agregando
  el tiempo de
• evolucion t1 nos da la segunda dmiension

90s
tm
90
t1
tm