Exemples

1
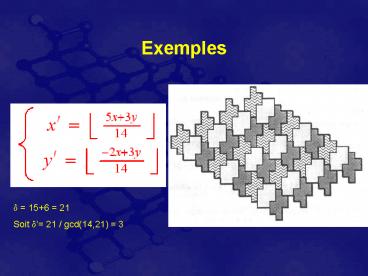
Exemples
d 156 21 Soit d 21 / gcd(14,21) 3
2
Exemples
d 56 11 Soit d 11 / gcd(11,11) 1
3
Applications Quasi-Affines
Definition Un pavé dordre 2 est lensemble des
points dont limage par lAQA appartient au pavé
dordre 1 pour lindice i,j
Il y a d2 pavés distincts à lordre 2
4
Exemples
d 11 2 Soit d 2 / gcd(2,3) 2
4 paves à lordre 2
5
Exemples
d 11 2 Soit d 2 / gcd(2,3) 2
8 pavés différents à lordre 3
6
Exemples
Ordre 2
Ordre 1
Ordre 3
Ordre 4
Ordre 5
Ordre 7
7
Applications Quasi-Affines
Definition application contractante Une
application affine est dite contractante pour une
constante de Lipschitz slt1 pour tout vecteur x,y
nous avons f(x)-f(y) ltsx-y avec . la
norme Euclidienne.
Théorème une application affine f qui est
contractante a un unique point fixe a tel que
f(a)a
8
Applications Quasi-Affines
Propriété AQA contractante Si lapplication
affine associée à une AQA F est strictement
contractante alors F est aussi contractante
en-dehors de la boule de rayon
9
Dynamique
Trajectoire du point (10,0)
La dynamique de lAQA est définie par la suite Xn
F(Xn-1)
10
Dynamique
Bassin attracteur un bassin attracteur dun
cycle limite est la réunion de tous les arbres
attachés au cycle.
Z2 est décomposée en bassin dattracteur
11
Dynamique

• Cycle Limite une suite Pn de longeur n telle
  que F(Pi)Pi1 pour iltn, et F(Pn)P1
• Racine un point dun cycle limite. Une racine
  non triviale est reliée à un arbre non limitée à
  sa racine.
• Arbre Pour une racine R appartenant à un cycle
  limite C, un arbre est lensemble des points P
  pour lequel il exist ngt0 tel que Fn (P)R et Fn-1
  (P) ? C.

12
Dynamique

• Point fixe Un point fixe pour une AQA P est un
  1-cycle
• Arbre isolé Arbre dun point fixe
• Cycle isolé Un cycle limite avec des racines
  toutes triviales.
• Feuille point P tel que F-1(P) ?

13
Dynamique

• a 1 unique point
  fixe (0,0)
• Pas dautres
  cycle limite.
  
• a 2
  points fixes (0,0) et (0,-1)
• Pas dautres cycles
  limites.
• a 5 points fixes
• (0,0)(-1,-1)(0,-1)(1,-1)(0,-2)

14
Dynamique

• a 32768 points fixes.
• a 1043
  3-cycles et lorigine comme
• point fixe

15
Dynamique
16
Dynamique
Autour de lorigine il y a un 3-cycle, 5-cycle,
7-cycle, 11 cycle, 15-cycle,
17
Dynamique
Seulement 1 seul bassin attracteur infini. La
couleur représente la distance à lorigine qui
est lunique point fixe.
18
Dynamique
Quatre bassins attracteurs infinis
19
Dynamique
La couleur donne la distance au point fixe
20
A propos des Aqas

• - Les AQAs donnent une idée de la dynamique de
  certains calculs en informatique.
• Les AQAs permettent de construire des
  transformations avec certaines propriétés
  (rotations bijectives par exemple).
• Les AQAs sont liées aux systèmes de numérations.
• Les AQAs permettent de construire des pavages.
• Les AQAs sont liées aux intersections de droites
  discrètes.

21
Exemples d AQA Rotations discrètes
bijectives
22
Rotation discrète classique
Rot(a)
Problème perte dinformation
23
Rotation discrète classique
Perte dinformation
24
Rotation pythagoricienne
Andres (1992)
with a2 b2 (b1)2
25
Rotation pythagoricienne
Théorème La rotation pythagoricienne est une
transformation discrète bijective
Evaluation de la qualité de la rotation
Distance max et min entre un point tourné par
les rotations discrètes et continues Max
0.707 average 0.3