Competition Models

1
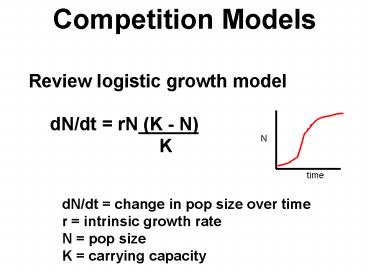
Competition Models
Review logistic growth model
dN/dt rN (K - N) K
dN/dt change in pop size over time r
intrinsic growth rate N pop size K carrying
capacity
2
Lotka Voltera Competition Equations
dN1/dt r1N1 (K1 - N1 - ?12 N2) K1
Species I
r1 intrinsic rate of increase for spp.1 N1 pop
size for spp. 1 K1 carrying capacity for spp.
1 N2 population size for spp 2 ?12 competition
coefficient (spp 1 effect on spp 2)
dN2/dt r2N2 (K2 - N2 - ?21 N1) K2
Species II
3
Graph displaying all possible combinations of N1
and N2
N2
N1
4
On the graph, draw zero isoclines for each
species. Zero isocline- line along which species
x neither increase nor decreases For N1,
Set dN1 0 d t
0 r1N1 (K1 - N1 - ?12 N2)
Then r10, or N10 or ... 0 K1 - N1
- ?12 N2 rearrange N1 K1 - ?12 N2
When N1 0 N2K1/ ?12 When N2 0 N1
K1
5
Graph displaying N1 zero isocline, and vectors
showing increase or decrease of N1
K1/?12
N2
K1
N1
6
Do the same thing for species II
For N2
Set dN2 0 d t
0 r2N2 (K2 - N2 - ?21 N1)
Then r20, or N20 or ... 0 K2 - N2
- ?21 N1 rearrange N2 K2 - ?21 N1
When N2 0 N1K2/ ?21 When N1 0 N2
K2
7
Graph displaying N2 zero isocline, and vectors
showing increase or decrease of N2
N2
N1
8

• Three Possible Outcomes of Competition
• One species drives other to extinction
• Either species wins depending on density
• Stable co-existence

9
A. One species wins (graphs showing both zero
isoclines)
K1 intraspecific inhibitory on itself larger than
K2 can exert on spp. 1 (ie spp. 2 is weak
competitor)
K1/?12
Spp. 1 exerts more effect on spp. 2 than spp. 2
can on itself (ie spp. 1 is strong competitor)
N2
K1
N1
N1
10
A. One species wins (graphs showing vectors)
K1/?12
N1
N2
N2
N2
N1
K1
N1
N1
11
A. One species wins (graphs showing vectors and
joint pop increase)
K1/?12
N1 drives N2 to extinction and attains own
carrying capacity
N2
K1
N1
N1
12
B. Either species wins (depending on initial
density)
Note gt both compete more
strongly with other species than they
do with themselves. gt
K1/?12
N2
K1
e.g. when spp is more aggressive toward others
than toward own species
N1
13
B. Either species wins (depending on initial
density)
N1
N2
K1/?12
N2
K1
N1
14
B. Either species wins (depending on initial
density)
Initial densities determine outcome
K1/?12
Unstable Equillibrium point
N2
K1
N1
Stable points
15
C. Stable Co-Existence
K1/?12
gt Both species have less effect on the other
species than they have on themselves. gt
(i.e. both weak competitors)
Stable equilibrium point
N2
K1
N1
16
Lotka-Volterra model Predictions A. Strong
interspecific competitors outcompete weak
interspecific competitors. B. When
interspecific comp. is more important than
intraspecific, the initial densities determine
outcome. C. When interspecific comp. is less
important than intraspecific, the species coexist.
17
Pros Makes sense Shown experimentally A.
Tillmams diatoms (1977). B. Parks flour
beetles (1962). C. Paines sea palm and mussel
(1979).
18

• Cons
• No time lags, overshoot
• How often are resources limited?
• r, K, , assumed to be constant (steady
  state)
• tells nothing about the mechanism
  (descriptive model)
• Assumes linear relationships