Keys

1
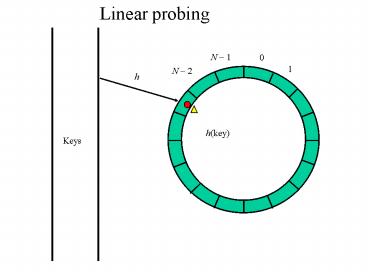
Linear probing
N - 1
0
1
N - 2
h
h(key)
Keys
2
Linear probing
N - 1
0
1
N - 2
h
(h(key) 1) mod N
Keys
3
Linear probing
N - 1
0
1
N - 2
h
(h(key) 2) mod N
Keys
4
Linear probing
N - 1
0
1
N - 2
h
(h(key) 3) mod N
Keys
5
Linear probing
N - 1
0
1
N - 2
h
(h(key) 4) mod N
Keys
6
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
Keys
7
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 1) mod N
Keys
8
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 4) mod N
Keys
9
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 9) mod N
Keys
10
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 16) mod N
Keys
11
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 25) mod N
Keys
12
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 36) mod N
Keys
13
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 49) mod N
Keys
14
Quadratic probing
N - 1
0
1
N - 2
h
(h(key) 81) mod N
Keys
15
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
h(key)
Keys
N 17 (prime)
16
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 1) mod N
Keys
N 17 (prime)
17
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 4) mod N
Keys
N 17 (prime)
18
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 9) mod N
Keys
N 17 (prime)
19
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 16) mod N
Keys
N 17 (prime)
20
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 25) mod N
Keys
N 17 (prime)
21
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 36) mod N
Keys
N 17 (prime)
22
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 49) mod N
Keys
N 17 (prime)
23
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 64) mod N
Keys
N 17 (prime)
24
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 81) mod N
Keys
N 17 (prime)
25
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 100) mod N
Keys
N 17 (prime)
26
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 121) mod N
Keys
N 17 (prime)
27
Quadratic probing
N - 1
0
1
N - 2
h
h(key)
(h(key) 144) mod N
Keys
N 17 (prime)
28
Quadratic probing
N 17 (prime)
Theorem If quadratic probing is used, and the
table size is prime, then a new element can
always be inserted if the table is at least half
empty.
N - 1
0
1
N - 2
h(key)
Proof In textbook, p. 192.
29
Quadratic probing
Theorem If quadratic probing is used, and the
table size is prime, then a new element can
always be inserted if the table is at least half
empty.
N 17 (prime)
N - 1
0
1
N - 2
h(key)
Application Probing visited only 9 of the 17
bins, but if the table is half empty, not all
those 9 bins can be occupied, so we must be able
to insert a new element in one of them.