Fr

1
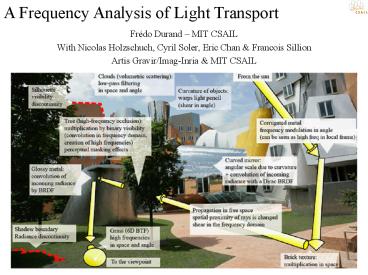
A Frequency Analysis of Light Transport

• Frédo Durand MIT CSAIL
• With Nicolas Holzschuch, Cyril Soler, Eric Chan
  Francois Sillion
• Artis Gravir/Imag-Inria MIT CSAIL

2
Frequency content matters in graphics

• Sampling, antialiasing
• Texture prefiltering
• Light field sampling
• Fourier-like basis
• Precomputed Radiance Transfer
• Wavelet radiosity, PRT
• Low-frequency assumption
• Irradiance caching

Image M. Zwicker
From Sloan et al.
Image H. Wann Jensen
3
Frequency content matters in vision

• Inverse lighting
• Shape from texture
• Shape from (de)focus
• See our Defocus Matting McGuire et al.

Rendering
Photograph
From Ramamoorthi Hanrahan 01
From Black and Rosenholtz 97
4
Goal Understand Frequency Content

• From the equations of light transport
• Spatial frequency (e.g. texture mapping)
• Angular frequency (e.g. blurry highlight)
• In a unified framework

5
Motivations

• Insights
• Derive sampling rates, filter bandwidth
• Rendering adaptive sampling
• Blurry objects
• Soft shadows
• PRT space vs. angle
• In particular shadows
• Light field sampling
• Non-Lambertian objects, occlusion
• Well-posedness of inverse problems

From Sloan et al.
6
Previous work

• Lots of related work
• Image antialiasing
• Ray differentials
• Perceptually-based rendering
• Wavelets for everything
• Fourier optics
• Tomography
• We focus on frequency analysis in graphics
• Texture pre-filtering
• Light field sampling
• Reflection as a convolution

Mitchell 1988
Gortler et al. 1993
Bolin et al. 1995
Sillion et al. 1991
Sillion et al. 1995
Ng et al. 2003
Hecht
Igehy 1999
7
Fourier optics

• We do not consider wave optics, interference,
  diffraction
• Only geometrical optics

From Hecht
8
Texture pre-filtering Heckbert 89

• Input signal texture map
• Perspective transforms signal
• Image resampling
• Fourier permits the derivation of filters
• Elliptical Weighted Average

minification
magnification
From Heckbert 1989
9
Light field sampling

• Chai et al. 00, Isaksen et al. 00, Stewart et
  al. 03
• Sampling rate and reconstruction filters
• Objects at depth d correspond to slope 1/d in
  light-field
• Lambertian, no occlusion

From Chai et al. 2000
10
Signal processing for reflection

• Ramamoorthi Hanrahan 01, Basri Jacobs 03
• Signal processing framework for reflection
• Light is the signal
• BRDF is the filter
• Reflection on a curved surface is convolution
• Direction only

From Ramamoorthi and Hanrahan 2001
11
Our approach

• Study frequency in both space and angle
• 4D radiance signal in neighborhood of ray
• Light sources are input signal
• Interactions are filters/transform
• Transport in free space
• Visibility
• BRDF
• Etc.
• Mostly theory,
• One proof-of-concept
• application

12
4 main effects

• Transport in free space
• Occlusion
• BRDF
• Curvature

13
Will be simpler in primal or Fourier

• Transport in free spaceboth
• Occlusion Primal
• BRDFFourier
• Curvatureboth

14
Local light field parameterization

• Around a central ray
• Follow this central ray during propagation
• 4D in 3D, 2D in 2D

Central ray
local light field
15
Local light field parameterization

• Around a central ray
• Follow this central ray during propagation
• 4D in 3D, 2D in 2D

angle v or q
space x
Central ray
local light field
16
Example point light

• Dirac in space
• Constant in angle

Ray space
v (angle)
x (space)
17
Example point light

• Dirac in space ) constant in Fourier
• Constant in angle ) Dirac in Fourier

Ray space
Fourier space
Wv (angle)
v (angle)
x (space)
Wx (space)
18
Example area light

• Box in space ) sinc in Fourier
• Constant in angle ) Dirac in Fourier

Ray space
Fourier space
Wv (angle)
v (angle)
x (space)
Wx (space)
19
Example scene
Receiver
Blockers
Light source
20
Example scene
Receiver
Blockers
After shading
Light source
After transport
At receiver
After occlusion
21
Transport
Ray space
Ray space
v (angle)
v (angle)
x (space)
x (space)
22
Transport
Ray space
Ray space
v (angle)
v (angle)
x (space)
x (space)
23
Transport
Ray space
Ray space
v (angle)
v (angle)
x (space)
x (space)
24
Transport

• Shear x x - v d

d
x
vd
v
x
Ray space
Ray space
v (angle)
v (angle)
x (space)
x (space)
25
Transport in Fourier space

• Shear in primal x x - v d
• Shear in Fourier, along the other dimension

Ray space
Ray space
Fourier space
Fourier space
Wv (angle)
Wv (angle)
Wx (space)
Wx (space)
Video
26
Transport ) Shear

• This should be reminiscent of light field
  spectraChai et al. 00, Isaksen et al. 00

From Chai et al. 2000
27
4 main effects

• Transport in free spaceshear(nice in both)
• Occlusion
• BRDF
• Curvature

28
Occlusion

• Consider planar occluder
• Multiplication by binary function
• Mostly in space

blocker function
Before occlusion
After occlusion
29
Occlusion in Fourier

• Multiplication in primal
• Convolution in Fourier (creates high frequencies)

Ray space
Ray space
blocker function
Fourier space
Fourier space
Wv (angle)
Wv (angle)
blocker spectrum
Wx (space)
Wx (space)
30
4 main effects

• Transport in free spaceshear(nice in both)
• Occlusionmulti/convoPrimal
• BRDF
• Curvature

31
Transport again
Ray space
Ray space
Fourier space
Fourier space
Wv (angle)
Wv (angle)
Wx (space)
Wx (space)
32
4 main effects

• Transport in free spaceshear(nice in both)
• Occlusionmulti/convoPrimal
• BRDF
• Curvature

33
BRDF integration

• For each spatial location
• For each outgoing direction
• Integration over incoming angles

x
34
BRDF integration

• For each spatial location
• For each outgoing direction
• Integration over incoming angles
• If BRDF is rotationally invariant
• Convolution Ramamoorthi 01

x
x
35
BRDF in Fourier

• Convolution ! multiplication

BRDF
Ray space
Ray space
Fourier space
Fourier space
Wv (angle)
Wv (angle)
Wx (space)
Wx (space)
BRDF spectrum
36
e.g. diffuse integration

• Convolve by cte!multiply by horizontal window
• Only spatial frequencies remain

Vertical cte
Ray space
Ray space
Fourier space
Fourier space
Wv (angle)
Wv (angle)
Wx (space)
Wx (space)
Horizontal window
37
Relation to previous work

• Ramamoorthi Hanrahan 01, Basri Jacob 03
• They consider a spatially-constant illumination
• But they dont have locality assumptions
• They work with spherical harmonics
• But essentially, nothing much changed

Fourier space
Ray space
38
Consequence on soft shadows

• When we make blockers smaller
• First we get more high-frequency content
• Then we get purely soft shadows!

39
Consequence on soft shadows
video

• Blockers scaled down ) spectrum scaled up
• With the shear, the lobe is pushed to angle
  frequencies

Main lobe due to characteristic frequency of
blockers
Fourier space
Wv (angle)
blocker spectrum
blocker function
Wx (space)
40
4 main effects

• Transport in free spaceshear(nice in both)
• Occlusionmulti/convoPrimal
• BRDFconvo/multiFourier
• Curvature

41
Curvature

• For each point x, the normal has a different
  angle
• Equivalent to rotating incoming light

Normal at x
x
Central normal
42
Curvature

• For each point x, the normal has a different
  angle
• Equivalent to rotating incoming light
• At center of space, nothing changed

Central normal
43
Curvature

• For each point x, the normal has a different
  angle
• Equivalent to rotating incoming light
• The further away from central ray,the more
  rotated

44
Curvature

• For each point x, the normal has a different
  angle
• Equivalent to rotating incoming light
• The further away from central ray,the more
  rotated

45
Curvature

• For each point x, the normal has a different
  angle
• Equivalent to rotating incoming light
• The further away from central ray,the more
  rotated
• This is a shear, but vertical

46
Curvature in Fourier

• Vertical shear in primal ! horizontal shear
  in Fourier

47
A fun example caustics

• Consider a solar oven
• Initially, directional source
• Ends up focused in space

48
4 main effects

• Transport in free spaceshear(nice in both)
• Occlusionmulti/convoPrimal
• BRDFconvo/multiFourier
• Curvatureshear (nice in both)

49
Swept under the rug

• Cosine term
• Multiplication/convolution
• Central incidence angle
• Scale in space
• And a couple of other technical detail

50
Also included in the theory

• Texture mapping (multiplication, convolution)
• Separable rotation varying BRDFs, Fresnel term
• Multiplicationconvolution ! convomulti
• Spatially-varying BRDF
• Fun semi Fourier transform

51
Extension to 3D

• It all works!
• See paper!

52
Whats fun in 3D? Anisotropy!

• Curvature (principal direction)
• Incident angle (along and across incidence plane)
• ! EWA for textures

53
Application proof of concept

• Adaptive sampling for Monte-Carlo ray tracing
• Based on image frequency content
• Blurry regions receive less samples
• Visibility evaluated densely
• Shading only is subsampled

54
Criteria

• BRDF bandwidth
• Curvature
• Occlusion
• Harmonic blocker distance
• In a single equation,expressed in imagebandwidth

Curvature BRDF
Blocker distance
55
Application to rendering

• Shading evaluated at 20,000 samples for a 800x500
  image uniform samples

56
Application to rendering

• Shading evaluated at 20,000 samples for a 800x500
  image with local bandwidth prediction

57
Sampling pattern
58
Summary frequency in space angle

• Transport in free space
• shear
• Occlusion
• multi/convo
• BRDF
• convo/multi
• Curvature
• shear
• Proof of conceptbandwidth prediction

59
Ongoing work

• More experimental validation on synthetic scenes
• Theory
• Bump mapping, microfacet BRDFs
• Sub-surface scattering
• Participating media (fog, clouds)
• Light field and auto-stereoscopic displays
• Wave optics
• Rendering applications
• Ray tracing
• Pre-computed radiance transfer spatial sampling
• Revisit traditional techniques
• Vision, statistics of natural images
• General theory of shape from X

Image Wann Jensen
From Flemin et al.
60
Acknowledgments

• Jaakko Lehtinen
• Reviewers of the MIT and Artis graphics groups
• Siggraph reviewers
• NSF CAREER award 0447561 Transient Signal
  Processing for Realistic Imagery
• NSF CISE Research Infrastructure Award
  (EIA9802220)
• ASEE National Defense Science and Engineering
  Graduate fellowship
• Realreflect IST project
• INRIA équipe associée
• MIT France

61
(No Transcript)
62
Why locality?

• Linearization
• ? ¼ tan ?
• Curvature
• Principle of uncertainty
• Cant measure frequency content on too-small a
  neighborhood
• Non-stationarity of scene
• Scene properties vary spatially, e.g. occluders,
  size of objects

63
Comparison to previous work

• Ray footprint
• Transport and curvature shear
• Light field sampling
• They mostly treat diffuse objects
• Convolution BRDF
• We treat space angle
• We separate cosine and BRDF
• Additional effects texture, separable BRDF,
  space-varying BRDF
• But we need to linearize
• On convolution
• Previous work found convolution in the primal
  where we have convolution in the dual
• We show that it is a special case

64
On convolution

• Previous work have used convolution where we use
  multiplication convolution
• Because they consider special cases (1D variation)