Simple coupled physicalbiogeochemical models of marine ecosystems

1
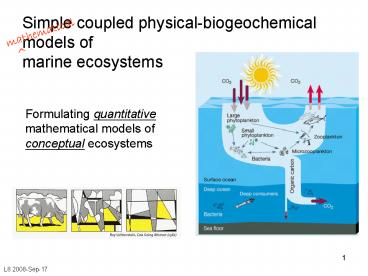
Simple coupled physical-biogeochemical models of
marine ecosystems
mathematical

• Formulating quantitative mathematical models of
  conceptual ecosystems

L8 2008-Sep-17
2
Why use mathematical models?

• Conceptual models often characterize an ecosystem
  as a set of boxes linked by processes
• Processes e.g. photosynthesis, growth, grazing,
  and mortality link elements of the
• State (the boxes) e.g. nutrient concentration,
  phytoplankton abundance, biomass, dissolved
  gases, of an ecosystem
• In the lab, field, or mesocosm, we can observe
  some of the complexity of an ecosystem and
  quantify these processes
• With quantitative rules for linking the boxes, we
  can attempt to simulate the changes over time of
  the ecosystem state

3
What can we learn?

• Suppose a model can simulate the spring bloom
  chlorophyll concentration observed by satellite
  using observed light, a climatology of winter
  nutrients, ocean temperature and mixed layer
  depth
• Then the model rates of uptake of nutrients
  during the bloom and loss of particulates below
  the euphotic zone give us quantitative
  information on net primary production and carbon
  export quantities we cannot easily observe
  directly

4
(No Transcript)
5
Reality Model

• Individual plants and animals
• Many influences from nutrients and trace elements
• Continuous functions of space and time
• Varying behavior, choice, chance
• Unknown or incompletely understood interactions

• Lump similar individuals into groups
• express in terms of biomass and CN ratio
• Small number of state variables (one or two
  limiting nutrients)
• Discrete spatial points and time intervals
• Average behavior based on ad hoc assumptions
• Must parameterize unknowns

6
The steps in constructing a model

• Identify the scientific problem(e.g. seasonal
  cycle of nutrients and plankton in mid-latitudes
  short-term blooms associated with coastal
  upwelling events human-induced eutrophication
  and water quality global climate change)
• Determine relevant variables and processes that
  need to be considered
• Develop mathematical formulation
• Numerical implementation, provide forcing,
  parameters, etc.

7
State variables and Processes

• NPZD model named for and characterized by its
  state variables
• State variables are concentrations (in a common
  currency) that depend on space and time
• Processes link the state variable boxes

8
Processes

• Biological
• Growth
• Death
• Photosynthesis
• Grazing
• Bacterial regeneration of nutrients
• Physical
• Mixing
• Transport (by currents from tides, winds )
• Light
• Air-sea interaction (winds, heat fluxes,
  precipitation)

9
State variables and Processes

• Can use Redfield ratio to give e.g. carbon
  biomass from nitrogen equivalent
• Carbon-chlorophyll ratio
• Where is the physics?

10
Examples of conceptual ecosystems that have been
modeled

• A model of a food web might be relatively complex
• Several nutrients
• Different size/species classes of phytoplankton
• Different size/species classes of zooplankton
• Detritus (multiple size classes)
• Predation (predators and their behavior)
• Multiple trophic levels
• Pigments and bio-optical properties
• Photo-adaptation, self-shading
• 3 spatial dimensions in the physical environment,
  diurnal cycle of atmospheric forcing, tides

11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
Examples of conceptual ecosystems that have been
modeled

• In simpler models, elements of the state and
  processes can be combined if time and space
  scales justify this
• e.g. bacterial regeneration can be treated as a
  flux from zooplankton mortality directly to
  nutrients
• A very simple model might be just N P Z
  
• Nutrients
• Phytoplankton
• Zooplankton all expressed in terms of
  equivalent nitrogen concentration

15
(No Transcript)
16
(No Transcript)
17
Mathematical formulation

• Mass conservation
• Mass M (kilograms) of e.g. carbon or nitrogen in
  the system
• Concentration Cn (kilograms m-3) of state
  variable n (mass per unit volume V)

18
Mathematical formulation
e.g. inputs of nutrients from rivers or sediments
e.g. burial in sediments
e.g. nutrient uptake by phytoplankton
The key to model building is finding appropriate
formulations for transfers, and not omitting
important state variables
19
Some calculus
Slope of a continuous function of x is
Baron Gottfried Wilhelm von Leibniz 1646-1716
20
Example f distance x time df/dx speed
Which comes from
21
State variables Nutrient and PhytoplanktonProce
ss Photosynthetic production of organic matter
Large N Small N
Michaelis and Menten (1913)
vmax is maximum growth ratekn is
half-saturation concentration at Nkn
f(kn)0.5
22
Representative results from 32Si kinetic
experiments measuring the rate of Si uptake as a
function of the silicic acid concentration
(ambientadded). Four of the 26
multi-concentration experiments are shown,
representing the main kinetic responses observed
in this study (Southern Ocean). Nelson et al.
2001 Deep-Sea Research Volume 48, Issues 19-20 ,
2001, Pages 3973-3995
23
Uptake expressions
24
State variables Nutrient and PhytoplanktonProce
ss Photosynthetic production of organic matter
The nitrogen consumed by the phytoplankton for
growth must be lost from the Nutrients state
variable
25

• Suppose there are ample nutrients so N is not
  limiting then f(N) 1
• Growth of P will be exponential

26

• Suppose the plankton concentration held constant,
  and nutrients again are not limiting f(N) 1
• N will decrease linearly with time as it is
  consumed to grow P

27

• Suppose the plankton concentration held constant,
  but nutrients become limiting then f(N) N/kn
• N will exponentially decay to zero until it is
  exhausted

28
Can the right-hand-side of the P equation be
negative? Can the right-hand-side of the N
equation be positive? So we need other
processes to complete our model.
29
(No Transcript)
30
There are many possible parameterizations for
processes e.g. Zooplankton grazing
Zooplankton grazing rates might be parameterized
as proportional to Z i.e. g constant or
if P is small the grazing rate might be less
because the Z have to find them or catch them
first
Ivlev (1945) function Grazing parameter Iv
31
Light
Irradiance I Initial slope of the P-I curve a
32
Coupling to physical processes

• Advection-diffusion-equation

turbulent mixing
Biological dynamics
advection
C is the concentration of any biological state
variable
33
I0
spring
summer
fall
winter
34
Simple 1-dimensional vertical model of mixed
layer and N-P-Z type ecosystem

• Windows program and inputs files are at
  http//marine.rutgers.edu/dmcs/ms320/Phyto1d/
• Run the program called Phyto_1d.exe using the
  default input files
• Sharples, J., Investigating theseasonal vertical
  structure of phytoplankton in shelf seas,
  Marine Models Online, vol 1, 1999, 3-38.

35
(No Transcript)
36
(No Transcript)
37
I0
spring
summer
fall
winter
bloom
38
I0
spring
summer
fall
winter
bloom
secondary bloom
39
I0
spring
summer
fall
winter
bloom
secondary bloom
40
(No Transcript)