GEM Project CrossCorrelations of WMAP5

1
GEM Project Cross-Correlations of WMAP-5
ForegroundsBruce Grossan, George Smoot GEM Team
Introduction The Galactic Emission Mapping, or
GEM project is a collaboration between UC
Berkeley / Berkeley Center for Cosmological
Physics (BCCP), the INPE of Sao Jose dos Campos
(Brazil), CENTRA - Centro Multidisciplinar em
Astrofísica (Portugal) and IT - Instituto de
Telecomunicações (Portugal), among others. The
project aims to provide (nearly) all-sky maps for
understanding of galactic foregrounds, with
several intensity and polarization maps planned
for this year and next. The GEM project is now
reducing maps and ramping up for analysis. This
poster describes preliminary work on reduction
with the GEM maps. As a beginning, we are
investigating if the correlations of our
intensity maps differ significantly from those in
nearby frequency channels. Several types of map
correlation measures are used in the literature
for separation of and/or limiting the
contribution of components. Before we used of
this type of tool, we wanted to test it. Some
correlation measures give only linear
relationships of data. Sky maps are often modeled
as a single foreground component Gaussian CMB.
It seems likely they are much more complicated!
Do correlation measures give useful information
for combinations of real, non-orthogonal,
non-Gaussian emission components? GEM
MAPS You are invited to view the other GEM
posters including GEM 2.3 GHz Map (Tello et al.
2008, submitted) - adds about 10 more sky to
Rhodes GEM 5 GHz Stokes Q,U
Maps (South only at this time) Ref
erence Key DF07 Dobler Finkbeiner, 2007
astro-ph/0712.2238 dOC04 de Oliveira-Costa et
al. 2004, ApJl 606,89 ( de Oliveira-Costa et a.
1997 ApJ 482,L17)B07 Bonaldi et al. 2007 MNRAS
382,1791

• More GEM Maps Coming
• (More Data is Better)
• Separation of real physical sky components is
  challenging via fitting and/or cross-correlation
  techniques with current data. More maps at more
  frequencies will produce better templates via
  improved restrictions on spatial variation of
  indices, and polarization maps will add another
  tool for separation of synchrotron and other
  polarized foregrounds. See below for details on
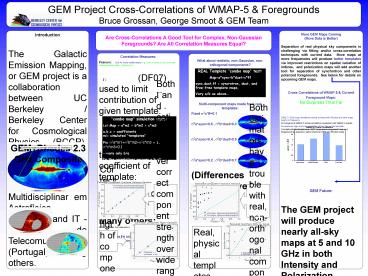
  upcoming GEM maps.
• Cross Correlations of WMAP-5 Current Foreground
  Maps
• No Surprises Thus Far
• GEM 2.3 GHz map correlations similar to those
  with Rhodes and other maps nearby in frequency.
• All Foreground,WMAP-5 cross-correlations
  consistent with WMAP-3 results -
• Anomalously high dust map correlation at low
  frequencies persists.
• Correlations with Bonaldi et al. 2007 "anomalous
  component" map and foregrounds as expected, same
  results for GEM and Rhodes maps.

Are Cross-Correlations A Good Tool for Complex,
Non-Gaussian Foregrounds? Are All Correlation
Measures Equal?

• Correlation Measures
• Pearson Only for linear relationships (e.g.
  even if obvious, but non-linear relation between
  data , Pearson0 !)
• ? (DF07) used to limit
  contribution of given template
• ?2(map,A) ?A2/?map2
• ? or â (dOC04) used to estimate
  coefficient of template
• map ?A cmb noise
• Many others e.g. ?struct -(K96) similar to
  above, but uses auto and cross-correlations to
  use structure information
• Can these be used for separation of
  multi-component foregrounds?
• Test with Gaussian Components

• What about realistic, non-Gaussian,
  non-orthogonal components?
• Multi-component maps made from real templates
• Fixed ?2cff0.1
• ?2async0.6 , ?2bdust0.3
• ?2async0.4 , ?2bdust0.5

REAL Template "combo map" test
Mapasyncbdustcff sync,dust,ff
syncrotron, dust, and free-free template
maps, Vary a/b as above
"combo map" simulation tests Let Map am1
bm2 cm3 a,b,c coefficientsmi simulated
"templates" Fix ?2am1?2bm2?2cm3 1,
?2cm30.1 -gtvary only b/a Do the correlations
recover a,b,c?
Both estimators have trouble with real,
non-orthogonal components.
Both ?and ? estimators recover correct component
strength over wide range of strengths.
Real, physical templates can be challenging to
fit - they are not orthogonal! More maps at more
frequencies would help differentiate the
templates more, and yield better coefficient
estimates.
Correct relative strength of components as well.