Normal%20distributions

1
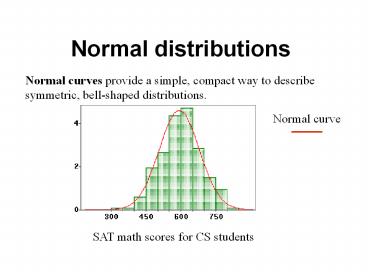
Normal distributions
Normal curves provide a simple, compact way to
describe symmetric, bell-shaped distributions.
Normal curve
SAT math scores for CS students
2
Money spent in a supermarket
Is the normal curve a good approximation?
3
SAT math scores for CS students
The area under the histogram, i.e. the
percentages of the observations, can be
approximated by the corresponding area under the
normal curve. If the histogram is symmetric, we
say that the data are approximately normal (or
normally distributed). We need to know only the
average and the standard deviation of the
observations!!
4
SAT math scores for CS students
The variable SAT math scores is normally
distributed with Mean m 595.28 and Std
Deviation s 86.40.
5
The standard normal curve
The standard normal distribution has mean 0 and
standard deviation 1 The curve is perfectly
symmetric around 0 Any value on a normal curve
can be converted to a value on the standard
normal curve using this formula (value mean)
/ standard deviation
6
Benchmarks under the standard normal curve
50
7
Graphing the normal curve using Excel

• Excel function NORMDIST area under the normal
  curve
• Syntax
• NORMDIST(x, m, s, 1) area to the left of x
• maverage sstandard deviation
• NORMDIST(x, m, s, 0) computes normal density
  function at x
• maverage sstandard deviation
• Excel function NORMSDIST(x,1) area under the
  standard normal curve (m0, s1)

8
Graphing the standard normal density curve

• Open a new workbook
• Enter the labels z and f(z) in cells A2 and B2
• Enter 3.5 -3.4 in cells A3 and A4, click and
  drag down until you create the sequence of digits
  from 3.5 to 3.5.
• Select B3 and enter NORMDIST(A3,0,1,0)
• Select B3 and drag down to B73
• Open the Chart Wizard, select XY (Scatter)
• The data range should already be indicated.

9
(No Transcript)
10
Normal distribution function F(z)

• It is defined as the area under the standard
  normal to the left of z, that is F(z)P(Zltz)

11
Application of the normal distribution to the data
Mean 595.28 Std Dev. s 86.40
The distribution of the SATM scores for the CS
students is approximately normal with mean 595.28
and s.d. 86.40 N(595.28 , 86.40)
Problem What is the percentage of CS students
that had SAT math scores between 600 and 750?
Answer Use the normal approximation - It is
the area under the normal density curve between
600 and 750.
12
How do we compute it?

• We use the values of the Normal distribution
  function F(x)P(Xltx).
• Problem What is the percentage of CS students
  that had SAT math scores between 600 and 750?
• Approximate answer
• The percentage of students with SATM between 600
  and 750 is computed as

600
600

750
__
750
595.28
595.28
595.28
13
Using Excel

• Select a cell, say A1
• Compute the area on the left of 600 as
• NORMDIST(600, 595.28 , 86.40, 1).
• Compute the area on the left of 750 as
• NORMDIST(750, 595.28 , 86.40, 1).
• The area under the curve between 600 and 750 is
• NORMDIST(750, 595.28 , 86.40,1)- NORMDIST(600,
  595.28 , 86.40, 600,1).
• The answer is 0.44 Approximately 44 of CS
  students in the survey have SATM between 600 and
  750.

14
In summary

• Follow the following steps
• State the problem. Calculate the sample average
  and the s.d. and define the interval you are
  interested in
• Compute the area under the approximate normal
  density curve with mean and s.d. defined above.

15
Example Problem
Problem What is the lowest SAT math score that a
student must have to be in the top 25 of all CS
students in the sample?
Mean 595.28 Std Dev. s 86.40
25
Sample Q3650
?
Find the value x, such that 25 of observations
fall at or above it.
16
Beware!
Is the normal approximation appropriate for these
data?
Overestimate this area
Underestimate this area
Use it when the histogram of the observations is
bell-shaped!