12'10 Two and threedimensional representations of fMRI data' PowerPoint PPT Presentation
1 / 36
Title: 12'10 Two and threedimensional representations of fMRI data'
1
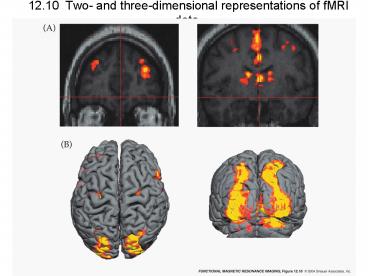
12.10 Two- and three-dimensional representations
of fMRI data.
2
12.12 Flat map views of the brain surface. (Part
1)
3
12.12 Flat map views of the brain surface. (Part
2)
4
12.11 Glass-brain views of fMRI data.
5
12.1 Statistical maps of fMRI data.
6
Statistics, more than most other areas of
mathematics, is just formalized common
sense. Paulos (1992)
7
What is statistics?
- Data require reduction and interpretation
- What do we do with a bunch of numbers?
- Statistics allow us to summarize and interpret
data. - Descriptive statistics
- Central tendency
- Variability
- Inferential statistics
- Significance testing
- Confidence intervals
8
Variability
- How spread out are the data?
- Tendency for the scores to differ from the
central tendency
9
8.1 How fMRI data are organized.
10
7.11 The first use of BOLD fMRI for functional
mapping of the human brain. (Part 2)
11
11.9 Within-conditions and between-conditions
variability in blocked fMRI data.
12
12.5 Conducting a t-test.
13
12.6 Assigning time points in a blocked design
to t-conditions.
14
7.12 Changes in BOLD activity associated with
presentations of single discrete events.
15
7.17(A) A sample fMRI time course from a single
voxel in the motor cortex.
16
7.17(B) Data from the individual trials that
make up Figure 7.17(A).
17
Sources of Variability ExampleFigure 11.15 (Part
2)
18
9.6 A map of noise across the brain.
19
10.6 Edge effects of head motion in fMRI
analyses.
20
9.7 Scanner drift.
21
12.4 The Students t-distribution.
22
12.2 Types of experimental errors.
23
Defining Probabilities
1- ?
?
?
1-?
- ? probability of a TYPE I error
- Type I when H0 is wrongly rejected
- ? probability of a TYPE II error
- Type II failing to reject H0 when it is actually
false
24
Defining Probabilities
- Relationship between ? and ?
25
Defining Probabilities
- Think in terms of H0 and H1 distributions
26
Power
- Power to detect a difference if it exists
- If H1 is true, how likely are you to reject H0?
- How good is your decision rule?
27
Factors Affecting Power
- Value of H1 (?0 - ?1)
- Size of ?
- Sample size
- Error variance
28
Value of H1 (?0 - ?1)
- With ?, N, and ? kept constant
Critical value
- Power increases as distance between the ?0 and ?1
increases
29
Effect of Changing ?
- With ?0 - ?1, N, and ? kept constant
- Power increases as ? increases
30
Effect of Variance
- With ?0 - ?1, ?, and N kept constant
Critical value
- Power increases as ? decreases
31
Effect of Sample Size
- With ?0 - ?1, ?, and ? kept constant
Critical value
- Power increases as N increases
32
Populations vs Samples
- Population--set of all possible members
- Every person/case that fits our interests is
accounted for - Equivalent to the space S
- Sample--subset of the population
- Selected group from the population
- Used to make estimates about the population
http//www.ruf.rice.edu/7Elane/stat_sim/sampling_
dist/index.html
33
Problems with samples
- Imperfect estimates of the population
- One must determine the quality of the estimate
coming from the statistics - Hence the 52 5
- This is where the theoretical distributions come
in to play - It is crucial to sample the population
appropriately
34
What can you actually do?
- ? difference between ?0 ?1 NOT USUALLY
- The differences are occurring in the real world
- Use higher field magnet?
- ? ? MAYBE
- Do you have a principled reason?
- Cost/Benefits analysis?
- ? Sample size YEP
- Unless it is practically impossible
- UPSHOT? Most things are beyond your control, but
you need to be aware of them
- ? Error variance MAYBE
- You might be able to tighten your design
- Increase number of trials?
- Use better measures?
35
Common Sense
- When we reject H0, we say the differences were
significant - What are significant results really telling us?
- Unlikeliness
- Surprise
- What is practically important?
- Why 0.05 or 0.01?
36
12.13 Basic principles of the general linear
model in fMRI.