16.360 Lecture 3

1
16.360 Lecture 3
Last lecture

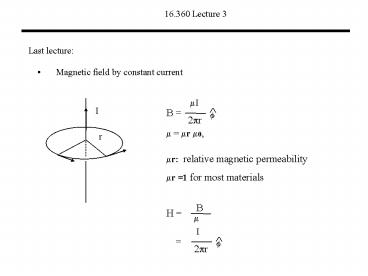
• Magnetic field by constant current

? ?r ?0,
?r relative magnetic permeability
?r 1 for most materials
2
16.360 Lecture 3
Last lecture

• Traveling wave

y(x,t) Acos(2?t/T-2?x/?),
y(x,t) Acos?(x,t),
?(x,t) 2?t/T-2?x/?,
3
16.360 Lecture 3
Last lecture

• Traveling wave

y(x,t) Acos(2?t/T2?x/?),
Velocity 0.6?/0.6T ?/T
Phase velocity
Vp dx/dt - ?/T
4
16.360 Lecture 3

• Phasor

VR(t)
Vs(t) V0Sin(?t?0),
VR(t) i(t)R,
Vs(t) VR(t) VC(t),
V0Sin(?t?0)
i(t)dt/C i(t)R,
Integral equation,
Using phasor to solve integral and differential
equations
5
16.360 Lecture 3

• Phasor

Vs(t) V0Sin(?t?0)
j(?0 - ?/2)
)
Re(V0 e
6
16.360 Lecture 3

• Phasor

1
),
Re(I
j?
time domain equation
V0Sin(?t?0)
i(t)dt/C i(t)R,
phasor domain equation
7
16.360 Lecture 3

• Phasor domain

V
I R
,
I
R 1/(j?C)

,
R 1/(j?C)
Back to time domain
j?t
Re (
e
)
R 1/(j?C)
8
16.360 Lecture 3

• An Example

VR(t)
Vs(t) V0Sin(?t?0),
VR(t) i(t)R,
Vs(t)
VL(t)
i (t)
Ldi(t)/dt,
VL(t)
Vs(t) VR(t) VL(t),
V0Sin(?t?0)
Ldi(t)/dt i(t)R,
differential equation,
Using phasor to solve the differential equation.
9
16.360 Lecture 3

• Phasor

j?t
di(t)/dt
Re(d I e
)/dt
j?
),
Re(I
time domain equation
V0Sin(?t?0)
Ldi(t)/dt i(t)R,
phasor domain equation
j?
)L
Re(I
10
16.360 Lecture 3

• Phasor domain

I R
j?L
V
I

,
I
R (j?L)

,
R j?L)
Back to time domain
j?t
Re (
e
)
R (j?L)
11
16.360 Lecture 3

• Steps of transferring integral or differential
  equations to linear
• equations using phasor.

1. Express time-dependent variables as phsaor.
2. Rewrite integral or differential equations in
   phasor domain.
3. Solve phasor domain equations
4. Change phasors variable to their time domain value

12
16.360 Lecture 3

• Electromagnetic spectrum.

Recall relation ?f v.

• Some important wavelength ranges

1. Fiber optical communication ? 1.3 1.5?m.
2. Free space communication 700nm 980nm.
3. TV broadcasting and cellular phone 300MHz
   3GHz.
4. Radar and remote sensing 30GHz 300GHz

13
16.360 Lecture 3

• Transmission lines

1. Transmission line parameters, equations
2. Wave propagations
3. Lossless line, standing wave and reflection
   coefficient
4. Input impedence
5. Special cases of lossless line
6. Power flow
7. Smith chart
8. Impedence matching
9. Transients on transmission lines

14
16.360 Lecture 3

• Today

1. Transmission line parameters, equations

B
A
VBB(t)
Vg(t)
VAA(t)
L
A
B
VAA(t) Vg(t) V0cos(?t),
Low frequency circuits
VBB(t) VAA(t)
Approximate result
VBB(t) VAA(t-td) VAA(t-L/c)
V0cos(?(t-L/c)),
15
16.360 Lecture 3

1. Transmission line parameters, equations

Recall ??c, and ? 2??
VBB(t) VAA(t-td) VAA(t-L/c)
V0cos(?(t-L/c)) V0cos(?t- 2?L/?),
If ?gtgtL, VBB(t) ? V0cos(?t) VAA(t),
If ?lt L, VBB(t) ?VAA(t), the circuit theory
has to be replaced.
16
16.360 Lecture 3

• Next lecture

1. Types of transmission lines
2. Lumped-element model
3. Transmission line equations
4. Wave propagation

17
(No Transcript)