Formal System Specification PowerPoint PPT Presentation
1 / 60
Title: Formal System Specification
1
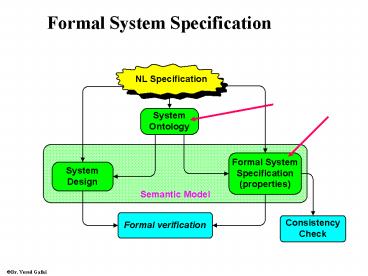
Formal System Specification
2
Formal System Specification
- Logic Based
- LTL - Propositional Linear Temporal Logic
- CTL Computational Tree Logic
- It is possible to employ automata based
specification - languages (will be presented later)
3
Overview of Logic
- Propositional Calculus
- Predicate Calculus
- Decision procedures
4
Propositional Calculus
- Syntax
- atoms p, q, r, and constant atoms tt,
ff. - every atom is a wff.
- if P, Q are wff then so are
- ?P, P?Q, P?Q, P ?Q, P ?Q
- Semantics an interpretation I p1,,pk ?
true, false. - I ??tt and not I ??ff
- I ??p iff I(p)true
- I ???P iff not I ??P
- I ??P?Q iff I ??P or I ??Q
- Model equivalencies P?Q ? ?(?P ? ?Q), P?Q?
?P ? Q
I ??f is called a model of f.
5
Satisfiability Validity
- f is satisfiable if I ??f for some I.
- f is valid if I ??f for all I ( ?? f).
Example valid formula (A ? (A?B)) ? B
A B A?B A ? (A?B)) (A ? (A?B)) ? B
F F T F T
T F F F T
F T T F T
T T T T T
6
Propositional Calculus in Practice
- Low expressive power
- Refers only to concrete objects
- No interpreted relations.
- For instance,
- Cubes a, b, c
- Relations are expressed by atoms
- aONb, aONc, aONc,
- that must be interpreted according to given
configuration
7
Predicate Calculus
- Vocabulary
- P - predicates, C - constants, X -
variables. - Language (wff)
- - Atoms tt, ff, p(v1,,vn) where p?P, vi?C
?X - - f, g ?wff, x?X ?f, f?g, ?x.f,
?x.f - Closed formula all variables are bounded
- Example
- ?x. x?7, ?x. Top(x) ? ??y. on(y,x)
8
Predicate Calculus Semantics
- Semantic domain
- D - a set of values (infinite),
- R - relations over D
- Interpretation I(IP,IC), IP P ? R, IC C?D
- Satisfaction (w.r.t. closed wff)
- - I ??p(c1,,cn) iff (IC(c1),,IC(cn))?IP(p).
- - I ???f iff not I ??f.
- - I ??f?g iff I ??f or I ??g.
- - I ???x.f iff I ??fx?d for all d?D.
- - I ???x.f iff I ??fx?d for some d?D.
9
System Specification
- System - set of constants (objects) a, b, c,
d, - System model relations on system objects
- ?x. ?on(x,x)
- ?x. ?y. ?(on(x,y) ? on(y,x))
- ?x. top(x) ? ??y. on(y,x)
- ?(?x. ? y. ? z x?y?z ? on(x,z) ? on(y,z))
- Requirements
- ?x. ?on(d,x), ?top(b)
- Design
- top(a), on(a,b), on(b,c), top(d)
A
B
C
D
Properties can be specified abstractly (no
reference to a concrete object)
10
Decidability
- Decision Procedure (satisfiability).
- ? Termination.
- ? Soundness if f is satisfiable returns yes.
- ? Completeness if returns yes then f is
satisfiable. - Note Satisfiability ? Validity
- f is valid iff ?f is not satisfiable.
11
Propositional Calculus Decidability
- Decidable
- Check all possible interpretations (2n).
- However there are more practical procedures.
12
Tableau Method for Propositional Calculus
- ? type wff - satisfied iff all of its
subformulae are satisfied. - ? type wff - satisfied if subsets of its
subformulae are satisfied.
? type A1 A2
p?q p q
??p p -
?(p?q) ?p ?q
?(p?q) p ?q
? type B1 B2
p?q p q,?p
p?q ?p p,q
p?q p,q ?p,?q
?(p?q) ?p p,?q
?(p?q) p,?q ?p,q
13
Tableau Algorithm for f (wwf)
- Construct a tree of nodes each contains a set F ?
sub(f) - 1. Start with the root node that contains f.
- 2. Repeat until nodes are close or do not
contain unchecked - components (open node).
- - For every node that contains an unchecked
?-wff g - construct a single subnode
- F-g ? g', A1(g), A2(g)
- - For every node that contains an unchecked
?-wff g - construct two sub-nodes
- F-g ? g', B1(g), F-g ? g', B2(g)
- - If any of the constructed nodes contains
wffs g and ?g, - mark it closed, and do not continue
expanding this node. - f is satisfiable iff there is an open leaf in the
tree
14
Examples
(A ? B) ? ?C
((A?B)??C), (A?B)
((A?B)??C), ?C
((A?B)??C), (A?B), A, B
A ? (B ? ?A)
(A?(B??A)), A, (B??A)
(A?(B??A)), A, ((B??A)), ?A
(A?(B??A)), A, (B??A),B
15
Showing validity of (((pq)?r)(p ?q)) ? (p ?r)
16
Predicate Calculus
Predicate calculus is in general
undecidable. However, there are decidable
subclasses (monadic predicates).
17
Temporal Logics
- Express reactive properties (order of events in
time) - - e.g. Always when a packet is sent it will
Eventually be received
- Linear Time Temporal Logic
- Every state has unique time successor
- Infinite sequences
- Computation Tree Logic
- A state may have multiple time successors
- Infinite tree
18
Propositional Linear Temporal Logic (LTL)
- Extension of propositional logic with temporal
operators. - Syntax
- - Atomic propositions a,b,c,, and constants tt,
ff - - For every formulae p,q
- ?p, p?q, Op, ?p, ?p, pUq
next
until
always
eventually
- Examples
- p?O?p, ?(p?O?p), ?(XisZero), (close)U(stop)
19
LTL Semantic Domain
- Semantic domain of LTL formula ?P
- ??, where ? 2P
- Namely an interpretation of ? is a sequence
- ?0, ?1, ?2, where ?i?2P for i1,2,
Notation ?0 ?, ?j ?j ?j1 ?j2, jgt0
20
LTL Semantics
?j??tt, ?j??ff ?j??tt, ?j??ff ?j??tt, ?j??ff
?j??p Iff p??j
?j???? iff ?j???
?j????? iff ?j??? or ?j???
?j??O? iff ?j1???
?j???? iff ? k?j ?k???
?j???? iff ?k?j s.t. ?k???
?j???U? iff ?k?j s.t. ?j?i?k ?i??? and ?k???
? is a model of ? iff ?0?? ?
21
LTL Examples I
- Op ?1??p
?p ?k?0 s.t. ?k ??p
?p ? k?0 ?k ??p
22
LTL Examples II
pUq ?k?0 s.t. ?0?i?k ?i ??p and ?k ??q
?(pUq) ?j?0 s.t. ?j??pUq, i.e.
?k?j s.t. ?j?i?k ?i ??p and ?k ??q
23
LTL interpretation over Transition Systems I
- Oq
- ?p
- ?u
- rUs
24
LTL interpretation over Transition Systems II
- ??s
- O(r?qUs)
25
Identities
- ?q ? ttUq
- ? ?? ttUq iff ?k?0 s.t. ?0?i?k ?i ??tt
and ?k ??q - iff ?k?0 s.t. ?k ??q
- iff ? ?? ?q
- ?q ? ???q (exercise).
- Hence, O, U form a compact set of temporal
operators
26
Common implications (tautologies)
- ?p ? ?q ? ?(p ? q)
- ?p ? ?q ? ?(p ? q)
- p ? ?p
- Op ? ?p
- ???p ? ??p
- ??? p ? ??p
- ?p ? ??p
- ??p ? ?p
- q ? pUq
- ?q ? ?(pUq)
idempotency
27
LTL ? ? regular language
- Defined w.r.t a given LTL formula ?.
- Let Patomic propositions that appear in ?
- Define ?2P
- By definition ???? for every model ? of ?,
- L?(?), the set of all models of ?, is an
?-regular language - proof by induction on the structure of
? - ? Is the converse ? regular language ? LTL,
true ?
28
Properties Classification
- Safety
- ?? - something bad never happens (actually
invariants) - - can be proved false within a finite
prefix of a run. - -- traffic and pedestrian lights never show green
simultaneously - ??(T_Green ? P_Green)
- no deadlock
- ?(action1 ? ? actionn)
- Liveness
- ?? - something good will happen
- can be proved false only along an
infinite run. - -- program termination
- Pstart ? ?Pterminates
29
Some Typical Property Patterns (I)
- Response
- p ? ?q initial p is followed by q
- ?(p?q) responsiveness
- ?(p? ?q) every p is followed by q
- Recurrence
- ??p infinitely often
- ??p eventually always
- Precedence
- pU(qUr) -- pqr??
- (pUq)Ur -- (pq)(rpp,rpq
pq,r)?? - (pUq)??p -- weak until
- ?pWq -- p cannot occur before q
p ? q ?def ?(p?q)
denoted by p ? ?q
pWq?def (pUq)??p
30
Some Typical Property Patterns (II)
- P is true between Q and following R
- ?((Q ? ?R ? ?R) ? PU(P?R)
- S precedes any occurrence of P before first
occurrence of R - ?R ? (?PU(S ? R))
31
Some Typical Property Patterns (III)
- S responds to P after Q
- ?QW(Q ? ?(P ? ?S))
- S followed by an occurrence of T occurs
before P - ?P ? (?PU(S ? ?P ? O(?PUT)))
32
Example Chained Until
- Between the time an elevator is called at a floor
and the time it opens its doors at that floor the
elevator can pass that floor at most twice. - Let
- Move ? ?(AtFloor?DoorOpen)
- Stop ? AtFloor ??DoorOpen
- Open ? AtFloor ?DoorOpen
- Then,
- ?((call ? ?Open)
- ? (Move U (Open ? (Stop U (Open
- ? (Move U
(Open ? (Stop U (Open -
? (Move U Open))))))))))
33
System Formalization with LTL
- Natural language ? formal language specification
- Formalization employs Conceptualization
- Primitive concepts (types)
- used to describe a certain kind of
systems - at a certain level of
abstraction. - Real-time systems conceptualization
- Event - occurs instanteneously (at any time
instant true or absent). - Condition Boolean variable (at any time
instanttrue or false). - Operation system reaction to input events
(necessarily terminating). - Duration - a time interval.
34
System Formalization Process
- Build system ontology
- The entities of a concrete system
represented in - terms of conceptualization
- system inputs events, variables
- system states conditions
- system reactions operations (system outputs)
- Specify system assumptions
- LTL formulae over system ontology
- Specify system requirements
- LTL formulae over system ontology
- Assumptions ? Program ? Requirements
Typed variables (at present assume only finite
domain)
35
Water Level Control (WLC)
valve
Water-level sensor
H
L
- The valve should be open as long as water level ?
L, and close - as long as water level ? H. An open valve, stays
open until - level ? H, similarly, a closed valve stays closed
until level ?L. - At startup, water level ? H.
36
WLC Ontology
Controller
Valve position command
Water-level sensor
H
valve
L
Input WaterLevel low, inter,
high Operations ValvePositionCmd
closed, opened
37
WLC Ontology Propositional Representation
- Interpreted by logic, hence use Booleans
- WaterLevel low, inter, high
- ? Conditions LowLevel,
InterLevel, HighLevel - ?(LowLevel ? InterLevel ? HighLevel)
- LowLevel ? ?(InterLevel ? HighLevel)
- InterLevel ? ?(LowLevel ? HighLevel)
- HighLevel ? ?(InterLevel ? LowLevel)
- ValvePositionCmd closed, opened
- ? Condition ValveClosed
tt-closed, ff-open - ? In practice, enumeration types are used and
proof systems - automatically deploy them into Booleans with
the proper - axioms (assumptions).
Ontological Assumptions
38
WLC Assumptions
- Given properties, relevant to the system
implementation - External environment (controlled process)
behavior - -- At startup water level lt H.
- HighLevel
- - Open valve will eventually raise water
to high level - ??(??ValveClosed ? ??HighLevel)
- ?(?ValveClosed ? ?HighLevel)
- Design dependent (sensors, actuators, processor,
etc.) - Ontological definitions, and abstract variables
- -- Like WaterLevel distribution
39
WLC Requirements
- The valve is open as long as water level ? L, and
close as long as water level ? H. - (HighLevel ?ValveClosed) ? (LowLevel
??ValveClose) - An open valve, stays open until level ? H,
similarly, a closed valve stays closed until
level ? L - ?ValveClose ? ?ValveClose W HighLevel
- ValveClose ? ValveClose W LowLevel
40
WLC Real Specification
- Environment Assumptions
- Change of valve state occurs at an interval, not
a time instant. - Given container volume, and rates of water inlet
and outlet flow.
41
Railroad Crossing
42
Case Study Railroad Crossing
- Design a controller that handles the passage of a
train in a one-way railroad - crossing. The plant consists of a pair of
reliable sensors that indicate train - entering and exiting the crossing region (XR), a
signal for entering trains, - and a gate for blocking passage of cars from a
side road. - We assume that at startup no train enters, is
already in, or exits XR. The - minimal delay between successive trains is 40
seconds, and incoming trains - do not traverse the signal as long as it shows
stop''. It takes a train 6 - seconds to arrive at the signal, and further
15-25 seconds to traverse the - crossing (depending on whether the train had to
stop at the signal, or not). - It is required that
- The gate is closed when a train moves in the gate
area (between the signal and the exit point). - The gate is open whenever the crossing is empty
for more than 10 seconds. - Every train that arrives at the signal is allowed
to continue beyond the signal within 10 seconds. - No train enters XR while another train is still
there.
43
Railroad Crossing
Train stoped for no more than 10 sec
opened when no train more than 10 sec
No less than 40 sec
6sec
(15-25)sec
closed when train in
Initially empty
No more than 1 train in XR
44
The Railroad Crossing Ontology
- Events
- Tin - Train enters XR
- Tout - Train exits XR
- Operations
- Up - Raising the gate up (opening)
- Down - Lowering the gate (closing)
- Stop - Signal turned to show stop
- Pass - Signal turned to show pass
45
Assumptions
- At startup no train enters, or exits XR.
- ?(Tin ? Tout)
- At startup no train is in XR.
- (?Tout)W(Tin ??Tout) ?
- 40 seconds minimal delay between trains ?
- It takes a train 6 seconds to arrive at the
signal ? - It takes a train 15 to 25 seconds to traverse
gate area ?
46
Inserting Time Model into LTL
- Adopt discrete time model (N).
- Detrmine time unit.
- States are fixed rate snapshots of the system.
s0 s1 s2 s3 s4 s5
0 1 2 3 4
5
Next State Next time instant
47
Expressing Durations in LTL
This approach makes the satisfaibility problem
EXPSPACE-hard
- Op - p holds after one time unit.
- OOp - p holds after two time units.
- Onp - p holds after n time units (O0pp ).
- Om,np ?def Omp ? Om1p ? ? Onp
- -- p holds continuously in the interval
m,n - Om,np ?def Omp ? Om1p ? ? Onp
- -- p holds sometimes in the interval
m,n
48
Assertions (revised)
- At startup no train enters, is in, or exits XR.
- ?(Tin ? Tout) ? is in XR ?
- 40 seconds minimal delay between trains.
- Tin ? O1,39?Tin
- It takes a train 6 seconds to arrive at the
signal. - Introduce abstract variable AtSignal - the
train - arrives at the signal - defined by
- Tin ? O6(AtSignal)
- It takes a train 15 to 25 seconds to traverse
gate - area ?
- We need to characterize the instant a
train enters the - critical section ! (either immediately,
if signal shows pass, - or after being stopped when signal turns
to show pass
49
Conditions (Abstract Variables)
- Represented by event that occurs iff the
condition is true - ShowStop - the signal shows stop (abstract
variable). - (Stop! ? ShowStop) ?
- (O(Stop!) ? (ShowStop ? O(?_at_Pass))) ?
O(ShowStop)
- Any operation K, let
- _at_K initiation event
- K! termination event of its execution.
50
Entering the Crossing
- EnterGR train passes the signal
- (EnterGR ? (AtSignal??Twait)) ?
- O(EnterGR) ?O(AtSignal ??Twait)?(Twait
?O(?Twait)) - Twait - train waiting at signal
- ((AtSignal ? ShowStop) ? Twait) ?
- (O(AtSignal ? ShowStop) ?
- (Twait ?
O(ShowStop))) ? O(Twait) - ShowStop - the signal shows stop.
- (Stop! ? ShowStop) ?
- (O(Stop!) ? (ShowStop ? O(?_at_Pass))) ?
O(ShowStop)
51
Past Since Operators
- Past
- ?? - ? occurred in the previous step
- - ?j?? ?? iff j?1 and ?j-1???
(?0?? ??) - Now, ShowStop can be defined as
- (Stop! ? (?ShowStop ? ?_at_Pass)) ? ShowStop
- Since
- ?S? - ? occurred in the past and since then ?
- - ?j?? ?S? iff ?0?k? j s.t. ?k??? and
?k?i ?j ?i??? - Now, ShowStop can be defined as
- (?_at_Pass)S(Stop!) ? ShowStop
52
EnterGr rewritten
- EnterGR train passes the signal
- EnterGR ? (AtSignal ? ShowPass) ? (?Twait ?
Pass) - Twait - train waiting at signal
- Twait ? (ShowStop)S(AtSignal ? ShowStop)
- ShowStop - the signal shows stop.
- ShowStop ? (?_at_Pass)S(Stop!)
- ShowPass - the signal shows pass.
- ShowPass ? (?_at_Stop)S(Pass!)
53
Assertions (revised)
- At startup no train is in XR ?
- 40 seconds minimal delay between trains.
- Tin ? O1,39?Tin
- It takes a train 6 seconds to arrive at the
signal. - Tin ? O6(AtSignal)
- It takes a train 15 to 25 seconds to traverse
gate - area.
- EnterGR ? O15,25Tout
54
Requirements
- Every train that arrives at the signal is allowed
to continue beyond the signal within 10 seconds. - AtSignal ? O0,10(?Twait)
- No train enters XR while another train is still
there. - Tin ? O(?TinUTout)
- The gate is closed when a train traverses GR.
- EnterGR ? ClosedUTout
- Abstract variable Closed - the gate is closed
(assumption) - Closed ? (?_at_Up)S(Down!)
55
Requirements (cont.)
- The gate is open whenever the crossing is empty
for more than 10 seconds. - Empty_10s ? Open
- Empty_10s - XR is empty at least 10
seconds. - Empty_10s ? (?Tin)S(Bempty_10s)
- Bempty_10s - XR is empty 10 seconds
(exactly) - (?10(Startup ?Tout) ? ?0,10(?Tin)) ? Bempty_10s
- Open - the gate is open
- Open ? (?_at_Down)S(Up!)
- Add ontology assumption
- Startup ? O??Startup, or Startup ? ??true
Assumptions
56
About Abstract Variables
- Tin ? O6(AtSignal) AtSignal can be replaced
by ?6(Tin) - (Stop! ? ShowStop) ?
- (O(Stop) ? (ShowStop ? O(?_at_Pass)))
? O(ShowStop) - (Stop! ? (?ShowStop ? ?_at_Pass)) ? ShowStop
- (?_at_Pass)S(Stop!) ? ShowStop
57
Design Assumptions
- Specify design constraints that are not
explicitly expressed - in the controller program (usually time
constraints), but - are essential in an attempt to prove its
correctness. - We may want to assume that signal operations are
actions (synchronous operations) - _at_Stop ? Stop!, _at_Pass ? Pass!,
- Hence, we use Stop, Pass as initiated
events. - We need specify deadline constraints for gate
operations - (_at_Up ? (?_at_Down)U(Up!) ? O0,10(Up!)) ?
O0,10(_at_Down)) - (_at_Down ? (?_at_UpU(Down!) ? O0,10(Down!)) ?
O0,10(Up!))
58
Counting in LTL (the N Train Assumption)
- Goal Direct expression of empty and busy XR
- Ground assumption
- The number of exits does not exceed the number
of entries. - Problem
- LTL is not expressive enough to allow
counting. - Possible solution
- Assume that there are at most N trains in the
system (makes sense in real world).
59
N Train Assumption
- Say N2 Tcr0, Tcr1, Tcr2 indicate 0,1,2 trains
in XR then - ?(Tcr0 ? Tcr1 ? Tcr2)
- Tcr0 ? ?(Tcr1 ? Tcr2)
- Tcr1 ? ?(Tcr0 ? Tcr2)
- Tcr2 ? ?(Tcr1 ? Tcr0)
- Tcr0 ? ?Tout
- Tcr0 ? ?Tin ? O(Tcr0)
- Tcr0 ? Tin ? O(Tcr1)
- Tcr1 ? Tin ? ?Tout ? O(Tcr2)
- Tcr1 ? Tout ? ?Tin ? O(Tcr0)
- Tcr1 ? (?(Tout ? Tin) ? (Tout ? Tin)) ? O(Tcr1)
- Tcr2 ? Tout ? ?Tin ? O(Tcr1)
- Tcr2 ? ?Tout ? ?Tin -- here we make the
restriction to N2 - Tcr2 ? (?Tout ? (Tout ? Tin)) ? O(Tcr2)
These are axioms that define the meaning of
Tcr0,Tcr1,Tcr2
60
Properties Specification
- - At startup no train is in XR
- Tcr0
- - No train enters XR while another train is
still there. - ?(?Tcr2)