Network threats and attacks

1
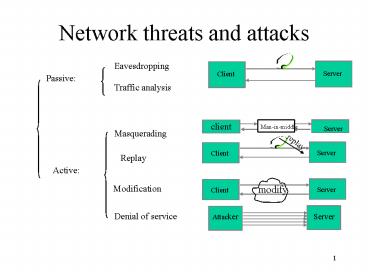
Network threats and attacks
Eavesdropping
Passive
Traffic analysis
Masquerading
Replay
Active
Modification
Denial of service
2
Security requirements and their implementation
encryption (and decryption)
Confidentiality
Integrity
checksum or hash value/message digest or MAC.
Authentication
user ID and password or Digital signature.
Nonrepudiation
Undeniable signature
Availability
Intrusion detection and defense
Authorization
Access control
Accountability
Log, record, trace, system administration
Q how to defense Replay attack?
Timestamps and/or sequence numbers.
3
Classification of cryptosystems

• Secret key (symmetric) vs. public key
  (asymmetric)
• Classical vs. modern
• Substitution vs. permutation (transposition)
• Monoalphabetic vs. Polyalphabetic
• Block vs. stream
• For stream cipher
• Synchronous vs. asynchronous (self-synchronizing)
  
• Periodic vs. non-periodic
• Dependent key stream vs. independent key stream

4
Classical (secret key) systems

• Substitution cipher
• Shift, Affine, Vigenere, Hill
• Permutation (transposition) cipher
• Stream cipher
• Binary stream cipher
• Autokey cipher
• One-time pad cipher
• Product of cryptosystems

5
Substitution cipherformal definition

• Let P C Z26 , K, consists of all possible
  permutations of the 26 symbols 0,1, , 25 ( or
  a,b,,z). For each permutation ? ?K, , define
• e?(x) ?(x)
• and
• d?(y) ?-1(y)
• (?-1 is the inverse permutation of ? )
• BACK

6
Permutation cipherformal definition

• Let m be a positive integer, Let P C (Z26)m
  and let K consists of all permutations of
  1,2,, m. For a key (i.e., a permutation) ?
• Define
• e?(x1,,xm) (x?(1),, x?(m))
• and
• d?(y1,,ym) (y?-1(1),, y?-1(m))
• Where ?-1 is the inverse permutation of ?.
• BACK

7
Shift cipherformal definition

• Let P C K, Z26 , for 0? K ? 25, define
• eK(x) x K mod 26
• and
• dK(y) y - K mod 26
• (x, y ? Z26 )
• BACK

8
Affine cipherformal definition

• Let P C Z26 and let
• K, (a,b) ? Z26 ? Z26
  gcd(a,26)1
• For K (a,b)? K, define
• eK(x)(axb) mod 26
• and
• dK(y)a-1(y-b) mod 26
• (x, y ? Z26 )
• BACK

9
Vigenere cipherformal definition

• Let m be an positive integer.
• Define P C K, (Z26)m.
• For each K (k1,k2,,km), define
• eK(x1,x2,,xm) (x1 k1, x2 k2,,
  xm km)
• and
• dK(y1,y2,,ym) (y1- k1, y2- k2,, ym- km)
• Where all operations are performed in Z26.
• BACK

10
Hill cipher formal definition

• Let m ? 2, be a positive integer. Let P C
  (Z26)m and let
• K, m?m invertible matrices over Z26
• For each key K, define
• eK(x) xK and dK(y) yK-1
• where all operations are performed in Z26.
• BACK

11
Stream cipher

• All previous ciphers encrypt plaintext elements
  using the same key, i.e., yy1y2eK(x1)eK(x2) .
  Called block cipher.
• On the contrary, stream cipher
• generate a keystream zz1z2
• use it to encryption i.e., yy1y2ez1(x1)ez2(
  x2)
• Synchronous stream cipher the keystream is
  constructed from the key, independent of
  plaintext text.
• Periodic stream cipher with period d if zid
  zi for i?1.
• Non-Synchronous stream cipher the keystream is
  constructed from plaintext text and/or
  ciphertext, as well as the key
• BACK

12
Binary Stream cipher

• In this case, P C Z2 and
• ez(x)(xz) mod 2 and dz(y)(yz) mod 2, i.e.,
  ez(x) and dz(y) use same exclusive-or operation.
• Suppose Kz0,,zm-1 c0,,cm-1, define
• Zmi ?m-1j0cjzij mod 2 for all i?1
• i.e., a key element is the linear combination of
  its previous m key elements.
• (z0,,zm-1) called initialization vector, cannot
  be (0,,0) and (c0,,cm-1) called coefficients
  with c01.
• BACK

13
Autokey cipher

• Let P C Z26 and let Kz1. Define zixi-1 for
  all i?2. (i.e, plaintext itself as key)
• For 0? z ? 25, define
• ez(x)(xz) mod 26
• and
• dz(y)(yz) mod 26
• (x,y ? Z26 ).
• BACK

14
One-time pad cipher
X x1x2xixn
xi ? ki yi
Kk1k2kikn
Yy1y2yiyn

• Synchronous, independent, non-periodic key stream
• The keystream length is same as the plaintext
  length
• A keystream is only used once.

BACK
15
Product of cryptosystems

• Consider an endomorphic cryptosystem
• The ciphertext space is the same as plaintext
  spcce.
• Suppose two ciphers S1 and S2
• Consider the cipher S1 ? S2
• e(k1,k2)(x) ek2(ek1(x))
• d(k1,k2)(y) dk1(dk2(y))
• Example
• shift cipher ? multiplicative cipher

16
Product of cryptosystems

• Commutive
• if S1 ? S2 S2 ? S1
• Associative (always)
• (S1 ? S2 )? S3 S1 ? (S2 ? S3 )
• Power of a cryptosystem
• S ? S S 2,
• S n, called iterated cipher.
• Idempotent
• S 2 S
• If S1 and S2 are both idempotent, then S1 ? S2
  is also idempotent.
• As a result, there is no gain for security when
  product two or more idempotent ciphers.
• Q are substitution and permutation ciphers
  idempotent?

17
Principles behind classical cryptosystems
Modular operation, multiplicative inverse
Extended Euclidean Algorithm
Prime, relative prime, Euler phi-function ?(n)
Matrix algebra
Permutation
Binary vector, binary operation , linear
combination,
Linear Feedback Shift Register
18
Cryptologycryptographycryptoanalysis

• Kerckhoffs principle
• Attack types
• Ciphertext only
• Known plaintext
• Chosen plaintext
• Chosen ciphertext

19
Attacks to classical cryptosystems
Known plaintext attack.
20
Models for evaluating security

• Unconditional security (perfect secrecy)
• Computational security
• Provable security
• Ad hoc security

21
Unconditional security

• Can not be broken under unlimited computing power
• Information-theoretic (probability theory)
  measure
• P(x/y)p(x)
• Necessary condition the key is at least as long
  as the message (e.g., one-time pad).
• Public key system is not unconditional security

22
Computational security

• The perceived level of computation to defeat it
  (using the best attack known) exceeds the
  computational resources of the hypothesized
  adversary.
• Related to supposed hard problem
• No proof
• Not NP-hard, not NP-complete
• Called practical security
• All current best known public key systems are
  this kind.

23
Provable security

• The difficulty of defeating it can be shown to be
  essentially as difficult as solving a well-known
  and supposedly difficult problem.
• A subclass of computational security

24
Ad hoc security

• The security depends on the concrete adversary
• Every successful attack requires a resource level
  (time space) greater than the fixed resource of
  a perceived adversary.

25
Key space

• A necessary condition (not sufficient) for a
  cryptosystem being secure is that the key space
  is large enough to beat the exhaust key search
  attack.
• How large it is? (Page 44)
• Example DES key space 256
• DES cracker take 56 hours to find a DES key
• 1998, 250,000, 1536 chips, 88 billion key/second
• DES challenge III
• DES cracker 100,000 computers, 22 hours, 15
  minutes
• 1999, 245 billion keys/second
• For security
• Key of 128 bits for secret systems
• Setting of numbers of 1024 bits for public systems

26
Mathematical principles for modern cryptography
.Group theory
Number theory
.Chinese remainder theorem (CRT), prime and
factorization
. Euler theorem
If b?Zn, b?(n) 1 mod n .
.Group and discrete logarithmic problem (DLP)
One-way function, trap-door function, hash
function.
Examples of one way functions (Page 9)
27
Modern (secret key) systems

• DES
• multiple round, permutation, transformation,
  S-box
• AES
• PGM
• Permutation group, logarithmic signature ?, ?.
• RC2, RC4

28
Public key cryptosystems
Cons and pros of secret and public key systems
(page 32)
Public key systems used for key management and
digital signature
Secret key systems used for encryption, data
integrity
RSA prime and factorization, CRT, Little
Fermat theorem ElGamal Zp, DLP Knapsack
knapsack and superincreasing knapsack Elliptic
curve Elliptic curve
29
Key management and exchange

• Key is the essential part in any cryptosystem.
• Diffie-Hellman key exchange (DLP)
• (Centralized) key distribution vs. (distributed)
  key agreement
• Public key infrastructure
• Public key certificate, certificate authority
• X.509 certificate architecture (hierarchical)

30
Hash functions and MAC
A computationally efficient function mapping
binary strings of Arbitrary length to binary
strings of some fixed length.
Three properties of hash functions
One-way,
Match-resistant,
Collision-resistant
Birthday attack
Two typical usages digital signature and data
integrity
Unkeyed hash function (MDC) vs. keyed hash
function (MAC)
MDC modification detection code, MAC message
authentication code
MD4, MD5, SHA-1, HMAC, DES-MAC
31
Digital signature
RSA signature, ElGamal signature, DSA/DSS
signature
32
Network security protocols

• IPSec (IP security)
• SSL (Secure Socket Layer) TLS
• SSH
• SFTP
• HTTPS, SHTTP
• PGP

Their similarities and differences

• PKI and X.509 certificate hierarchical CAs.

• Kerkeros

33
Secure group communication

• Key management
• Key tree scheme
• N-party Diffie-Hellman key agreement

34
Security and attack analysis of modern
cryptosystems

• Linear analysis and differential analysis
• Factorization
• Solving DLP problem
• The relationship between them
• Efficiency and performance
• 128 bits for secret systems
• 1024 bits for public systems