Data Compressing Codes (Communications Block Diagram) - PowerPoint PPT Presentation
1 / 13
Title:
Data Compressing Codes (Communications Block Diagram)
Description:
Ch04: Computer Arithmetic * 1 of 12. Data Compressing Codes (Communications Block Diagram) ... Ch04: Computer Arithmetic * 5 of 12. Statistical Redundancy ... – PowerPoint PPT presentation
Number of Views:245
Avg rating:3.0/5.0
Title: Data Compressing Codes (Communications Block Diagram)
1
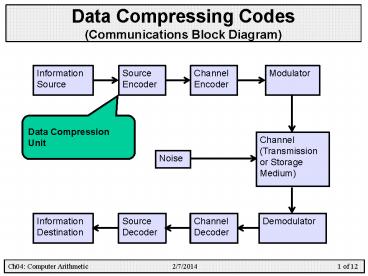
Data Compressing Codes(Communications Block
Diagram)
Information Source
Channel Encoder
Modulator
Source Encoder
Data Compression Unit
Channel (Transmission or Storage Medium)
Noise
Information Destination
Source Decoder
Channel Decoder
Demodulator
2
Data-Compressing CodesDefinitions
- Data compression (or source coding )
- is the process of encoding information using
fewer symbols than an unencoded representation
would use through use of specific encoding
schemes . - Lossless compression
- Attempts to remove statistically redundant
information from the source data. The source data
is recovered perfectly from the encoding. - Lossy compression
- Attempts to remove perceptually irrelevant
information from the source data. Removing the
irrelevant information tends to increase the
redundant information, making data compression
possible. The source data is recovered
imperfectly from the encoding.
3
Data-Compressing CodesDefinitions
- Compression Ratio
- Uncompressed sizecompressed size
- Example uncompressed size 1024 bits,
compressed size 256 bits. Therefore, the CR is
41
4
What is Statistical Redundancy?
- Most real-world data has statistical redundancy.
- Statistical redundancy is generally non-trivially
embedded in data. - Statistical redundancy appears as patterns hidden
in the data. - Data compression is achieved by encoding the
patterns instead of the actual data. - The encoding of patterns requires less symbols.
- The problem of data compression is to find the
hidden patterns, extract them, and then encode
them efficiently.
5
Statistical Redundancy Locator Run-Length
Encoding (RLE)
- Runs of data are stored as a single data value
and count, rather than as the original run. - For example, consider a screen containing plain
black text on a solid white background. - Let us take a hypothetical single scan line, with
B representing a black pixel and W representing
white - WWWWWWWWWWWWBWWWWWWWWWWWWBBBW . . .
- RLE yields the code
- 12WB12W3B24WB14W
- Twelve W's, one B, twelve W's, three B's, etc.
- CR is 6716.
6
Statistical Redundancy Locator Symbol
Probabilities
- For example, in English text,
- The letter e is much more common than the
letter z. - The probability that the letter q will be
followed by the letter z is very small. - It would be inefficient to encode each symbol
with the same size of codeword.
7
Statistical Redundancy Locator Huffman Code
- Construct a code that assigns frequently used
source-symbols short codes, and infrequently used
source-symbols longer codes. - Variable length codeword.
- Average codeword length
8
Huffman Code Average Length of Codeword
- Fixed Length Codeword System
- Let SL Symbol Length.
- (1/n)SUM(i1n) SLi SL, where SLi symbol
length of codeword i. - Variable Length Codeword System
- Note (1/n)SUM(i1n) SLi SUM(i1n)(1/n)SLi
, where (1/n) represents the equal probability
of a symbol appearing in a message. - SUM(i1n)(Pi )SLi , where Pi is the
probability of symbol i appearing in a message. - Average Length SUM(i1n)Pi SLi
9
Huffman CodeExample Alphabet A,B,C,D,E,F
Symbol Code
A 0
B 10
C 110
D 1110
E 1111
1x0.5000 2x0.2500 3x0.1250 4x0.0625 4x0.0625 1.875
Average Codeword Length 1.875 bits per symbol
10
Huffman CodeExample Alphabet A,B,C,D,E
0
Symbol Code
A 00
B 01
C 10
D 11
A 0.25
0
0.5
B 0.25
1
1.0
0
C 0.25
1
0.5
D 0.25
1
Average Codeword Length 2 bits per symbol
11
Statistical Redundancy Locator Quad trees
12
Statistical Redundancy Locator Quad trees
CR is 6429
13
What is Perceptual Irrelevancy?
- Information that is not relevant to the observer.
- Examples,
- Image, moving pictures, audio, speech.
- Removing irrelevant information increase the
amount of redundant information. - Consider an image 1024x1024 pixels that have
values within the range from 0000 0000 to 0001
1001. The average human visual system cannot
distinguish these pixels. - RLE can represent the entire image using 3 bytes
(00, 0400)