fMRI: Biological Basis and Experiment Design Lecture 20: Motion compensation PowerPoint PPT Presentation
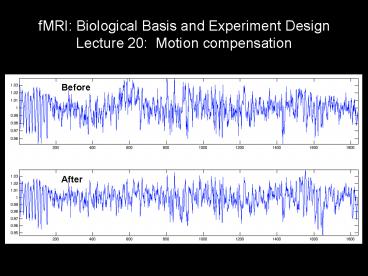
Title: fMRI: Biological Basis and Experiment Design Lecture 20: Motion compensation
1
fMRI Biological Basis and Experiment
DesignLecture 20 Motion compensation
Before
- Rotation matrices
- Effects on data
- Examples
After
1 light year 5,913,000,000,000 miles?
2
Rotation matrices
Two-dimensional rotation
y
cos(? ) sin (? ) -sin(? ) cos(? )
R
x
?
r (x,y)
r' R r
r'
3
An aside matrix multiplication
y Ax
A1,1 A1,2 A1,3 ... A1,n A2,1 A2,2 A2,3
... A2,n A3,1 A3,2 A3,3 ... A3,n . .
. Am,1 Am,2 Am,3 ... Am,n
A is an m x n matrix
x1,1 x1,2 x2,1 x2,2 x3,1 x3,2 . .
. xn,1 xm,2
x is an n x p matrix
4
An aside matrix multiplication
y is m x p
x is n x p
A is m x n
A1,1 A1,2 A1,3 ... A1,n A2,1 A2,2 A2,3
... A2,n A3,1 A3,2 A3,3 ... A3,n . .
. Am,1 Am,2 Am,3 ... Am,n
x1,1 x1,2 x2,1 x2,2 x3,1 x3,2 . .
. xn,1 xm,2
x
5
Rotation matrices
Two-dimensional rotation
y
cos(? ) sin (? ) -sin(? ) cos(? )
R
x
?
r (x,y)
r' R r
r'
cos(? ) sin (? ) -sin(? ) cos(? )
x y
x cos(? ) y sin (? ) -x sin(? ) y cos(? )
r'
6
Rotation example 45 degree rotation of r (1,1)
Two-dimensional rotation
y
r (1,1)
cos(45? ) sin (45? ) -sin(45? ) cos(45?
)
R
? 45?
x
r' (?2,0)
r' R r
1/?2 1/?2 - 1/?2 1/?2
1 1
1/?2 1/?2 -1/?2 1/?2
2/?2 0
r'
x
7
Rotation example parabola (ICE10.m)
8
Three dimensional rotation
Excerpt from Wolfram MathWorld
9
Affine transformation
(Wikipedia)
10
Output of MoCo algorithms
Strong activation affects center of mass
calculation
11
Effect of MoCo increased activation size
Before
After
12
Effect of MoCo voxels maintain identity
Before
After
13
(No Transcript)
14
(No Transcript)
15
Oakes et al., Fig. 1 6
16
(No Transcript)
17
Interpolation in motion correction
uncorrected
corrected
PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.
You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.
About the Developers
PowerShow.com is brought to you by CrystalGraphics, the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.