Discussion

1
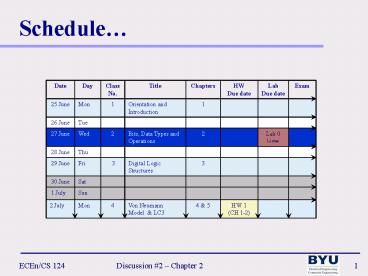
Schedule
2
Numbered

• Moses 133,35,37
•   33 And worlds without number have I created
  and I also created them for mine own purpose and
  by the Son I created them, which is mine Only
  Begotten.
•   37 And the Lord God spake unto Moses, saying
  The heavens, they are many, and they cannot be
  numbered unto man but they are numbered unto me,
  for they are mine
• 35 all things are numbered unto me, for they
  are mine and I know them.
• 3 Nephi 1831
• 31 behold I know my sheep, and they are
  numbered.

3
Chapter 2 Bits, Data Types, and Operations
4
Digital vs. Analog

• Wristwatches (numbers vs. hands)
• LPs vs. CDs
• Rotary phone vs.
• Cell phone
• NTSC vs. HDTV
• Slide rule vs.
• calculator
• 737s vs. 777s

5
Digital vs. Analog
Analog
Digital
6
Digital vs. Analog
Digital signals are limited to a set of possible
values (precision)
Set of 10 different symbol values ? decimal
Set of 2 different symbol values ? binary
7
Number Representations

• Decimal means that we have ten digits to use in
  our representation (the symbols 0 through 9)
• Example What is 3,546?
• three thousands five hundreds four tens six
  ones.
• 3,54610 3?103 5?102 4?101 6?100
• How about negative numbers?
• We use two more symbols to distinguish positive
  and negative, namely, and -.

8
Number Representations

• Example1 What is 1011.101?

9
Number Representations

• Example1 What is 1011.101?
• Depends on what radix or base we use
• Decimal base 10 (digit set
  0, 1, 2, 3, 4, 5, 6, 7, 8 , 9)
• Binary base 2 (digit
  set 0, 1)
• Hexadecimal base 16 (digit set 0,
  1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
  D, E, F)
• Other? base r (digit set
  0, r-1)

10
Etymologically Correct Base Names

• 2 - binary
• 3 - ternary
• 4 - quaternary
• 5 - quinary
• 6 - senary
• 7 - septenary
• 8 - octal
• 9 - nonary
• 10 - denary, although this is never used instead
  decimal is the common term.
• 11 - undenary
• 12 - duodenary, although this is never used
  duodecimal is the accepted word.
• 16 - senidenary, although this is never used see
  the discussion in hexadecimal.
• 20 - vegesimal
• 60 - sexagesimal

11
Number Representations

• Example1 What is 1011.101?
• Depends on what radix or base we use
• Decimal base 10 (digit set
  0, 1, 2, 3, 4, 5, 6, 7, 8 , 9)
• Binary base 2 (digit
  set 0, 1)
• Hexadecimal base 16 (digit set 0,
  1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
  D, E , F)
• Other? base r (digit set
  0, r-1)
• For base 10
• 1011.10110 1?103 0?102 1?101 1?100
  1?10-1 0?10-2 1?10-3
• For base 2
• 1011.1012 1?23 0?22 1?21 1?20
  1?2-1 0?2-2 1?2-3
• For base r
• 1011.101r 1?r3 0?r2 1?r1 1?r0
  1?r-1 0?r-2 1?r-3

12
Binary Numbers

• Binary means that we have two digits to use in
  our representation
• the symbols 0 and 1
• Example What is 10112?
• one eights zero fours one twos one ones.
• 10112 1?23 0?22 1?21 1?20

13
Binary Numbers
Bit a single binary symbol (i.e. a 0 or a 1)

• Bits rely only on approximate physical values.
• A logical 1 is a relatively high voltage (1.2V
  - 5V).
• A logical 0 is a relatively low voltage (0V -
  1V).

Byte a sequence of 8 bits
14
Whats in a Bit?

• A bit can take on one of two logical values
• 1
• 0
• Bit values are represented by various physical
  means.
• Voltages
• Residual magnetism
• Light
• Electromagnetic Radiation
• Polarization

15
Binary Numbers

• Numbers are represented by a sequence of bits
• A collection of two bits has four possible values
  or states00, 01, 10, 11
• A collection of three bits has eight possible
  states000, 001, 010, 011, 100, 101, 110, 111
• A collection of n bits has 2n possible states.
• By using groups of bits, we can achieve high
  precision.
• 8 bits gt number of states 256.
• 16 bits gt number of states 65,536
• 32 bits gt number of states 4,294,967,296
• 64 bits gt number of states 18,446,744,073,709,
  550,000

16
The Power of the Bit

• Analog processing relies on exact values which
  are affected by temperature, age, etc.
• Analog values are never quite the same.
• Each time you play a vinyl album, it will sound a
  bit different.
• CDs sound the same no matter how many times you
  play them.
• Digital processing relies on approximate physical
  values that are not affected by age, temperature,
  etc.
• Music that never degrades.
• Pictures that never get dusty or scratched.
• Disadvantage bits can only represent discrete
  values
• Digital Discrete

17
What Kinds of Data?

• All kinds
• Numbers signed, unsigned, integers, floating
  point,complex, rational, irrational,
• Text characters, strings,
• Images pixels, colors, shapes,
• Sound pitch, amplitude,
• Logical true / false, open / closed, on / off,
  
• Instructions programs,
• Data type
• representation and operations within the computer
• Well start with numbers

18
Data Types
Data Type a way to represent data and describes
ways to perform operations on that data

• Bits alone dont give information they must be
  interpreted
• Data types are what interpret bits
• Example interpret the following bits
• 0100 1000 0100 0101 0101 1000 0100 0001
• The integers 1850110 and 2259310?
• The characters H E X A ?
• The floating-point number 202081.01562510?
• Other?

19
Some Important Data Types

• Unsigned integers
• 0, 1, 2, 3, 4,
• Signed integers
• , -3, -2, -1, 0, 1, 2, 3,
• Floating point numbers
• PI 3.14159 x 100
• Characters
• 0, 1, 2, , a, b, c, , A, B,
  C, , _at_, ,

20
Unsigned Integers

• Weighted positional notation
• 3 is worth 300, because of its position, while
  9 is only worth 9

3x100 2x10 9x1 329
1x4 0x2 1x1 5

• What do these unsigned binary numbers represent?

0000 0110
1111 1010
0001 1000
0111 1100
1011 1001
21
Unsigned Integers

• What numbers can be represented with 3 bits?

22
Unsigned Integers

• What numbers can be represented with 3 bits?

23
Unsigned Binary Arithmetic

• Base-2 addition just like base-10!
• add from right to left, propagating carry

10010 10010 1111 1001 1011 1 11011
11101 10000 10111 111
0
1
1
1
1
Subtraction, multiplication, division,
24
Signed Binary Integers

• 3 common representations for signed integers
• Sign magnitude
• 1s compliment
• 2s compliment

Most common for computers
25
Signed Binary Integers

• Determine the range of values for n bits

• n bits ? 2n distinct values

½ for negative values
½ for positive values
BUT need a symbol for zero
26
Sign-Magnitude

• Range
• Representations
• 01111binary gt 15decimal
• 11111 gt -15
• 00000 gt 0
• 10000 gt -0
• Problem
• Difficult addition/subtraction
• check signs
• convert to positive
• use adder or subtractor as required
• How to add two sign-magnitude numbers?
• Ex 1 (-4)

The MSB encodes the sign 0 1 -
27
Why we do not use signed magnitude
28
How to Add Signed-Magnitude Numbers
29
1s Complement

• Range
• Representations
• 00110binary gt 6decimal
• 11001 gt -6
• 00000 gt 0
• 11111 gt -0
• Problem
• Difficult addition/subtraction
• no need to check signs as before
• cumbersome logic circuits
• end-around-carry
• How to add to ones complement numbers?
• Ex 4 (-3)

To negate a number, Invert it, bit-by-bit. MSB
still encodes the sign 0 1 -
30
2s Complement

• Problems with sign-magnitude and 1s complement
• two representations of zero (0 and 0)
• arithmetic circuits are complex
• Twos complement representation developed to make
  circuits easy for arithmetic.
• only one representation for zero
• just ADD the two numbers to get the right answer
  (regardless of sign)

31
2s Complement

• Range
• Representation
• If number is positive or zero,
• normal binary representation, zeroes in upper
  bit(s)
• If number is negative,
• start with positive number
• flip every bit (i.e., take the ones complement)
• then add one

MSB still encodes the sign 0 1 -
32
2s Complement Representation

• What is 01101012 in decimal?
• What is its 2s complement?

33
2s Complement Representation

• What is 01101012 in decimal?
• What is its 2s complement?
• 01101012 0?26 1?25 1?24 0?23 1?22
  0?21 1?20
• 5310

34
2s Complement Representation

• What is 01101012 in decimal?
• What is its 2s complement?
• 01101012 0?26 1?25 1?24 0?23 1?22
  0?21 1?20
• 5310

0110101 (53) 1001010 (1s comp)
1 1001011 (-53)
35
2s Complement

• Positional number representation with a twist
• the most significant (left-most) digit has a
  negative weight
• n-bits represent numbers in the range -2n-1
  2n-1 - 1
• What are these?

0110 22 21 6
1110 -23 22 21 -2
0000 0110 1111 1010 0001
1000 0111 1100 1011 1001
36
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
37
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
MSB
38
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
MSB remaining bits
39
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
1
MSB remaining bits
40
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
1
MSB remaining bits
11111111
41
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
1
MSB remaining bits
11111111
42
2s Complement

• Positional number representation with a twist
• MSB has a negative weight

0110 22 21 6
1110 -23 22 21 -2
1
MSB remaining bits
1
11111111 -27 26 25 24 23 22 21 20
43
2s Complement Shortcut

• To take the twos complement of a number
• copy bits from right to left until (and
  including) the first 1
• flip remaining bits to the left

011010000 011010000 100101111 (1s
comp) 1 100110000 100110000
(copy)
(flip)
44
2s Complement Negation

• To negate a number, invert all the bits and add 1

6 1010
7 1001
0 0000
-1 0001
4 1100
-8 1000 (??)
45
Decimal to Binary Conversion

• Positive numbers
• start with empty result
• if decimal number is odd, prepend 1 to result
  else prepend 0
• divide number by 2, throw away fractional part
  (INTEGER divide)
• if number is non-zero, go back to else you are
  done
• Negative numbers
• do above for positive version of number and
  negate result.

46
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

47
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

48
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 195/2 97.5 ? 97
49
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 97/2 48.5 ? 48
50
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 48/2 24
51
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 24/2 12
52
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 12/2 6
53
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 6/2 3
54
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 3/2 1.5 ? 1
55
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

Integer division by 2 1/2 0.5 ? 0
56
Binary Numbers Decimal to Binary

• Example convert -195 to 2s complement binary
  notation

• First find positive version (195) in binary
  then take 2s complement

0110000112
2s complement
1001111012
57
Decimal to Binary Conversion
0101
0110
01111011
00100011
11011101
01111101111
58
Adding 2s Complement Integers
00110 00101 01011
00110 -00101 00001

• You can get overflow
• the result cannot be represented by the number of
  bits available

0110 0101 1011
Hmmm. 6 5 ¹ -5. Obviously something went
wrong. This is a case of overflow.

• For 2s Complement overflow happens when
• 2 positive numbers add to form a negative number
• 2 negative numbers add to form a positive number

59
Binary Numbers

• Review

60
Binary Numbers

• Review

61
Sign-Extension in 2s Complement
What do these represent?
6
0110 000000000000000110 1111
11111111111111111 1
6 (zero-extend ZEXT)
-1
-1 (sign-extend SEXT)
-1

• You can make a number wider by simply replicating
  its leftmost bit as desired.

62
Overflow Revisited

• Overflow the result doesnt fit in the capacity
  of the representation
• ALUs are designed to detect overflow
• Its really quite simple
• if the carry in to the most significant position
  is different from the carry out from the most
  significant position then overflow occurred.
• We will ignore most overflows in this course

63
Use SEXT To Prevent Overflow

• What is 1310 2910 ?
• How many bits should we use for each number?

001101 (13) Sign extended 100011
(-29) Sign extended 110000 (-16)
64
Word Sizes

• In the preceding slides, every bit pattern was a
  different length (15 was represented as 01111).
• Every real computer has a base word size
• word 16-bits (2 bytes) or 32-bits (4-bytes)
• Depends on processor
• our machine this semester has a word size of
  16-bits
• Memory fetches are word-by-word
• even if you only want 8 bits
• Instructions are packed into words like all data
• All numeric representations are word-sized
• 15 is represented as 0000000000001111

65
Logical Operations on Bits
A B AND 0 0 0 0 1 0 1 0 0 1 1 1
A B OR 0 0 0 0 1 1 1 0 1 1 1 1
A NOT 0 1 1 0
A B XOR 0 0 0 0 1 1 1 0 1 1 1 0
a 001100101 b 110010100
a AND b 000000100
a OR b 111110101
NOT a 110011010
A XOR b 111110001
66
Examples of Logical Operations

• AND
• useful for clearing bits
• AND with zero 0
• AND with one no change
• OR
• useful for setting bits
• OR with zero no change
• OR with one 1
• NOT
• unary operation -- one argument
• flips every bit

11000101 AND 00001111 00000101
11000101 OR 00001111 11001111
NOT 11000101 00111010
67
Floating Point Numbers

• Binary scientific notation
• 32-bit floating point
• Exponent is biased
• Implied leading 1 in mantissa

1
8
23
s
exponent
mantissa (or fraction)
68
Floating Point Numbers

• Why the leading implied 1?
• Always normalize after an operation
• shift mantissa until leading digit is a 1
• can assume it is always there gt dont store it
• Why the biased exponent?
• To avoid signed exponent representations

69
Floating Point Numbers

• Example Represent the number -6.625 x 223 in
  floating point representation.

70
Floating Point Numbers

• Example Represent the number -6.625 x 223 in
  floating point representation.
• Sign bit 1 (since the number is negative)

71
Floating Point Numbers

• Example Represent the number -6.625 x 223 in
  floating point representation.
• Sign bit 1 (since the number is negative)
• Fraction 6.62510 110.1012
• shift 2 to the left to get a leading 1
• gt 1.101012 x 22

72
Floating Point Numbers

• Example Represent the number -6.625 x 223 in
  floating point representation.
• Sign bit 1 (since the number is negative)
• Fraction 6.62510 110.1012
• shift 2 to the left to get a leading 1
• gt 1.101012 x 22
• Exponent (2) 23 127 14210 100011102

73
Floating Point Numbers

• Example Represent the number -6.625 x 223 in
  floating point representation.
• Sign bit 1 (since the number is negative)
• Fraction 6.62510 110.1012
• shift 2 to the left to get a leading 1
• gt 1.101012 x 22
• Exponent (2) 23 127 14210 100011102

N 1 10001110 10101000000000000000000
74
Floating Point Numbers

• What does this represent?

1 10000001 10101000000000000000000
The final number is -1.6563 x 22 -6.625
75
Hexadecimal Notation

• Binary is hard to read and write by hand
• Hexadecimal is a common alternative
• 16 digits are 0123456789ABCDEF

Binary Hex Dec 0000 0 00001 1 10010
2 20011 3 30100 4 40101 5 50110 6
60111 7 71000 8 81001 9 91010 A
101011 B 111100 C 121101 D 131110
E 141111 F 15
0100 0111 1000 1111 0x478F 1101 1110 1010 1101
0xDEAD 1011 1110 1110 1111 0xBEEF 1010 0101
1010 0101 0xA5A5

• Separate binary code into groups of 4 bits
  (starting from the right)
• Translate each group into a single hex digit

76
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

77
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
78
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
D
79
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
4
D
80
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
4
D
F
81
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
4
D
F
8
82
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
4
D
F
8
A
83
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
7
4
D
F
8
A
3
NB add a leading zero to complete 4 bits
84
Binary Numbers Hexadecimal

• Example convert 0111010100011110100110101112 to
  hexadecimal notation

011101010001111010011010111
0x3A8F4D7
This is not a new machine representation,just a
convenient way to write the number.
85
Binary Numbers Hexadecimal

• Properly sign-extending is important if the
  binary number is signed

10 1100 1001 0101
86
Binary Numbers Hexadecimal

• Properly sign-extending is important if the
  binary number is signed

10 1100 1001 0101
5
9
C
E/2
87
Decimal to Hex Conversion

• Positive numbers
• start with empty result
• next digit to prepend is number modulo 16
• divide number by 16, throw away fractional part
• if new number is non-zero, go back to else you
  are done
• Negative numbers
• do above for positive version of number and
  negate result.

88
Decimal to Hex Examples
12decimal 1100 0xc 21decimal
0001 0101 0x15 55decimal 0011 0111
0x37 256decimal 0001 0000 0000
0x100 47decimal 0010 1111
0x2f 3decimal 0011
0x3 127decimal 0111 1111
0x7f 1029decimal 0100 0000 0101 0x405
89
ASCII Codes

• How do you represent characters? A
• ASCII is a set of standard 8-bit (byte) codes to
  do this
• 32, 0 48, 1 49, A 65, B 66
• Zero-extended (ZEXT) to word size
• To convert an integer digit to ASCII character,
  add 48 (0)
• 1 48 49 gt 1

90
ASCII Characters
91
Interesting Properties of ASCII Code

• What is relationship between a decimal digit
  ('0', '1', )and its ASCII code?
• What is the difference between an upper-case
  letter ('A', 'B', ) and its lower-case
  equivalent ('a', 'b', )?
• Given two ASCII characters, how do we tell which
  comes first in alphabetical order?
• Are 128 characters enough?(http//www.unicode.org
  /)

No new operations -- integer arithmetic and logic.
92
Transmitting Characters
A 65 Decimal 0x41
A
0000 0000 0100 0001
A
93
Data Types
Data Type a way to represent data and describes
ways to perform operations on that data

• Bits alone dont give information they must be
  interpreted
• Data types are what interpret bits
• Example interpret the following bits
• 0100 1000 0100 0101 0101 1000 0100 0001
• The integers 1850110 and 2259310?
• The characters H E X A ?
• The floating-point number 202081.01562510?
• Other?

94
LC-3 Data Types

• Some data types are supported directly by
  theinstruction set architecture (ISA).
• For LC-3, there is only one hardware-supported
  data type
• 16-bit 2s complement signed integer
• Operations ADD, AND, NOT