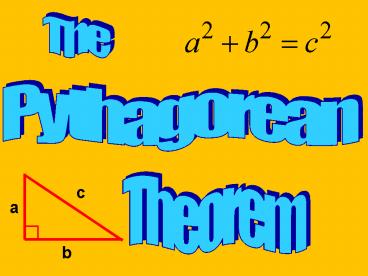The Pythagorean Theorem - PowerPoint PPT Presentation
1 / 47
Title:
The Pythagorean Theorem
Description:
About 2,500 years ago, a Greek mathematician named Pythagoras discovered a special relationship that exists between the three sides of every right triangle. – PowerPoint PPT presentation
Number of Views:281
Avg rating:3.0/5.0
Title: The Pythagorean Theorem
1
The
Pythagorean
Theorem
c
a
b
2
This is a right triangle
3
We call it a right triangle because it contains a
right angle.
4
The measure of a right angle is 90o
90o
5
The little square
in the
angle is telling you that it is a
right angle.
90o
6
About 2,500 years ago, a Greek mathematician
named Pythagoras discovered a special
relationship that exists between the three sides
of every right triangle.
7
Pythagorus realized that if you have a right
triangle,
8
when you square the lengths of the two sides that
make the right angle,
9
and then add the squares together,
10
the sum is the same value you get when you square
the longest side.
11
Is that correct?
?
Does
?
v
12
It is, and the same is true for any right
triangle.
v
13
The two sides which come together in a right
angle are called
14
The two sides which come together in a right
angle are called
15
The two sides that together form the right angle
are called
the LEGS.
16
The lengths of the legs are usually labeled a and
b.
a
b
17
The side across from the right angle
is called the
hypotenuse.
a
b
18
And the length of the hypotenuse
is usually labeled c.
c
a
b
19
The relationship Pythagoras discovered is now
called The Pythagorean Theorem
c
a
b
20
The Pythagorean Theorem states that, given a
right triangle with legs a and b and hypotenuse
c,
c
a
b
21
then . . .
c
a
b
22
then . . .
c2
c
a2
a
b
b2
23
then . . .
52
25
42
16
4
5
3
32
9
24
You can use The Pythagorean Theorem to solve many
kinds of problems.
Suppose you drive directly west for 48 miles,
48
25
Then turn south and drive for 36 miles.
48
36
26
How far are you from where you started?
48
36
?
27
Using The Pythagorean Theorem,
48
482
362
c2
36
c
28
Why?
Can you see that we have a right triangle?
29
Which side is the hypotenuse?
Which sides are the legs?
30
Then all we need to do is calculate
v v
60 c
31
And you end up 60 miles from where you started.
So, since c2 is 3600, c is
48
36
60
32
Find the length of a diagonal of the rectangle
?
33
Find the length of a diagonal of the rectangle
?
b 8
c
a 15
34
(No Transcript)
35
Find the length of a diagonal of the rectangle
17
36
Practice using The
Pythagorean Theorem to solve these right
triangles
37
13
38
(No Transcript)
39
Think
c2
b2
a2
40
So
c2
-
a2
b2
41
(a)
(c)
42
(a)
(c)
262
b2
102
43
(a)
(c)
676
-
b2
100
44
(a)
(c)
b2
576
24
v
45
24
(a)
(c)
c2
676
v
b2
576
a2
100
46
Your Turn!
a2 b2 c2
(a)
a 12
c 15
9
Awesome!
(c)
(b)
a2 b2 c2
(12)2 b2 (15)2
(144) b2 (225)
b2 (225) - (144)
b2 81
b v81
47
Your Turn!
a 24
b 32
Find the length of the diagonal.
32 in
a2 b2 c2
(b)
(24)2 (32)2 c2
24 in
(a)
40
(c)
(576) (1024) c2
c2 (1600)
c 40
The length of the diagonal is 40 inches.